Enunciado
Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 14.Problemas - Ex. 87
A Agência de Proteção Ambiental está investigando uma fábrica de produtos químicos abandonada. Um tanque cilíndrico grande e fechado contém um líquido desconhecido. Você precisa determinar a densidade e a altura do líquido no tanque (a distância vertical da superfície do líquido até o fundo do tanque). Para manter diversos valores da pressão manométrica no ar que está acima do líquido no tanque, você pode usar ar comprimido. Você faz um pequeno furo no fundo da lateral do tanque, que está sobre uma plataforma de concreto - para que o furo esteja 50,0 cm acima do solo. A tabela a seguir oferece suas medições da distância horizontal R que o fluxo de líquido inicialmente horizontal, jorrando para fora do tanque, trafega antes de atingir o solo e a pressão manométrica do ar no tanque.
(a) Represente graficamente em função de . Explique por que os pontos de dados ficam próximos de uma linha reta. Encontre a inclinação e a interceptação dessa linha. (b) Use a inclinação e a interceptação encontradas no item (a) para calcular a altura h (em metros) do líquido no tanque e a densidade do líquido (em ). Use . Suponha que o líquido seja não viscoso e que o furo seja pequeno o suficiente em comparação com o diâmetro do tanque para que a variação em h durante as medições seja muito pequena.
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”
Bora atacar esse problemaaaaaaa junto comigoo.
Para resolvermos essa questão, serão necessários os conhecimentos sobre pressão sobre um fluido e a distância que ele atinge em função de tal pressão.
- O gráfico de em função de está representado, a equação esta evidenciada na imagem
- Para calcular a altura do fluido, primeiramente devemos encontrar a distância em função da pressão,
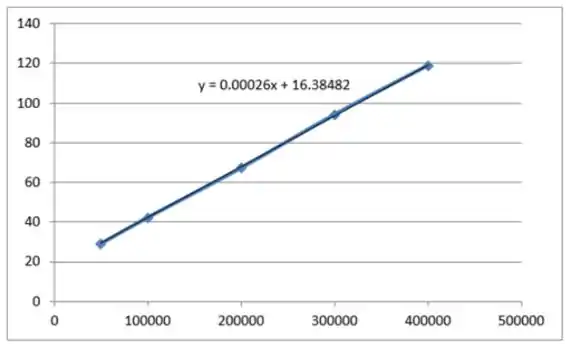
A inclinação da reta é igual a , e a interseção com o eixo y vale . O gráfico se apresenta próximo de uma reta, visto que, pela equação de Bernoulli, a distância, que está representado pela velocidade, se encontra elevado ao quadrado, enquanto a pressão do fluido é elevada a 1. Por isso tal gráfico se assemelha bastante a uma reta.
Portanto, conclui – se que a inclinação vale , e a interseção com o eixo y vale .
Passo 2
O intervalo de tempo é para a queda livre de uma altura de 50 cm acima do solo, ou seja, será igual a:
Passo 2
E a pressão será igual à soma entre a pressão do líquido com a pressão manométrica, ou seja, a equação se resume a:
Utilizando a interseção com o gráfico, podemos calcular a altura do nível da água, e com a inclinação, a densidade.
Portanto, a altura de líquido vale e a densidade vale
“Às vezes é preciso aprender a correr antes de começar a andar”
Resposta
- Portanto, conclui – se que a inclinação vale , e a interseção com o eixo y vale .
- Portanto, a altura de líquido vale e a densidade vale .