Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 89
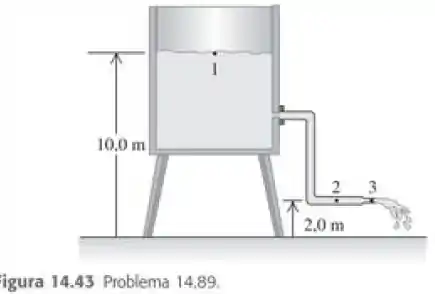
A água flui continuamente de um tanque aberto, como indicado na Figura 14.43. A altura do ponto 1 é 10,0 m e os pontos 2 e 3 estão a uma altura de 2,0 m. A área da seção reta no ponto 2 é igual a ; no ponto 3 ela é igual a . A área do tanque é muito maior do que a área da seção reta do tubo. Supondo que a equação de Bernoulli seja aplicável, calcule a) a vazão volumétrica em metros cúbicos por segundo; b) a pressão manométrica no ponto 2.
Passo 1
Aqui aplicaremos a equação de Bernoulli e a equação de continuidade.
O exemplo 14.8 diz que a velocidade do fluxo é calculada por , onde é a distância entre o furo e a superfície do fluido.
Passo 2
(a) A vazão volumétrica é calculada então por:
Onde:
Então:
Passo 3
(b) Lembrando que a pressão manométrica é a diferença entre a pressão no ponto e a pressão atmosférica (). Vamos usar Bernoulli nos pontos 2 e 3 para achar .
Aqui vem o pulo do gato: como está em contato com a atmosfera (pois está numa extremidade aberta para o ar), podemos calcular para achar a pressão manométrica em 2, pois:
Com isso, a pressão manométrica no ponto 2 é:
Só que , então podemos cortar os termos com as alturas:
Com isso:
Passo 4
Para achar , vamos usar o princípio da continuidade:
Passo 5
Substituindo na equação de Bernoulli:
Colocando em evidência:
Substituindo o valor de que achamos no passo 2 e os valores das áreas dados pelo enunciado:
Fazendo essas contas: