Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 2.Problemas - Ex. 3

3. Um reservatório contém água até 0,5   m de altura e, sobre a água, uma camada de óleo de densidade 0,69   g / c m 3 , também com 0,5   m de altura. Abre-se um pequeno orifício na base do reservatório. Qual é a velocidade de escoamento da água?

Passo 1

Bora lá pro nosso primeiro probleminha de hidrodinâmica do M ó y s e s !

Bom! Primeiramente vamos fazer um esboço dessa situação:

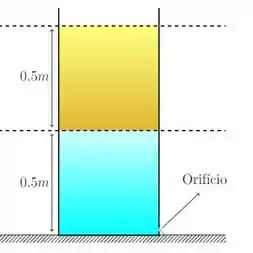
Baseado nessa figura, vamos determinar o quanto vale a pressão na base de nosso recipiente. Olha só! A pressão na base é exercida pela contribuição da coluna de óleo e da coluna de água, ambas de mesma altura, h = 0,5   m :

P = P 0 + ρ ó l e o g h + ρ á g u a g h = P 0 + ( ρ ó l e o + ρ á g u a ) g h

Passo 2

Com isso, escrevendo B e r n o u l l i   para o fluido na base do orifício e para o jato de água escoando...

P + ρ g h + ρ v 2 2 = C o n s t a n t e

Temos que na base do orifício, a velocidade do fluido é praticamente nula. Já quando a água sai do orifício, ela está exposto à pressão P 0 e correndo com uma velocidade v 0 . Sendo assim, nossa equação de B e r n o u l l i vai ficar assim...

P = P 0 + ρ v 0 2 2

Só que a pressão P na base do fluido, é dada por:

P = P 0 + ( ρ ó l e o + ρ á g u a ) g h

E assim, ficamos com a seguinte igualdade:

P 0 + ρ ó l e o + ρ á g u a g h = P 0 + ρ á g u a v 0 2 2

ρ ó l e o + ρ á g u a g h = ρ á g u a v 0 2 2

v 0 = 2 ρ ó l e o + ρ á g u a g h ρ á g u a

Substituindo os valores numéricos de cada variável, obtemos então, a nossa resposta:

v 0 = 2 0,69   g / c m 3 + 1,00 g / c m 3 ( 9,81   m / s 2 ) ( 0,5   m ) 1,00 g / c m 3

v 0 = 4,07   m / s

Resposta

V e l o c i d a d e   d e   e s c o a m e n t o → v 0 = 4,07   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tração de uma corda que mantém um bloco totalmente imerso em um líquido (de massa específica maior que a do bloco) é T 0 quando o recipiente está em repouso. Por qual fator é multiplicada a tração T
Uma esfera com raio de 6,22c m e massa 8,60k g está a uma profundidade de 2,22k m em água do mar com massa específica 1025k g / m 3 . Determine (a) a pressão manométrica, (b) a pressão total e (c) a f
A água flui continuamente de um tanque aberto, como indicado na Figura 14.43. A altura do ponto 1 é 10,0 m e os pontos 2 e 3 estão a uma altura de 2,0 m. A área da seção reta no ponto 2 é igual a 0,04
O tubo horizontal mostrado na Figura 14.45 apresenta seção reta com área igual a 40,0 c m 2 em sua parte mais larga e 10,0 c m 2 em sua constrição. A água flui no tubo, e a vazão volumétrica é igual a
A água de um grande tanque aberto com paredes verticais possui uma profundidade H (Figura 14.42). Um orifício é aberto na parede vertical a uma profundidade j abaixo da superfície da água. a) Qual é a