Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 93
Um líquido escoando por um tubo vertical apresenta uma forma definida durante escoamento. Para obter a equação para essa forma, suponha que o liquido esteja em queda livre quando sai do tubo. No exato momento em que ele sai, o liquido possui velocidade e o raio da corrente é . a) Encontre a expressão para a velocidade do liquido em função da distancia y de sua queda. Combinando essa relação com a da continuidade, ache uma expressão para o raio da corrente em função de y. b) Se a água escoa de um tubo vertical com velocidade de 1,20 m/s, a que distância da saída do tubo o raio será igual à metade do seu valor na corrente original?
Passo 1
Aplicaremos as equações de aceleração constante ao líquido em queda para encontrar sua velocidade em função da distância abaixo da tomada. Em seguida, aplicaremos a equação
para relacionar a velocidade com o raio do fluxo.
Seja o ponto 1 no final do tubo e deixe o ponto 2 estar no fluxo do líquido a uma distância 2 anos abaixo do final do tubo,
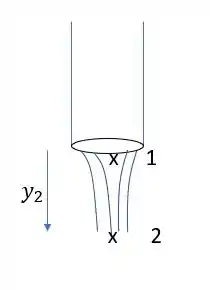
Considere a queda livre do líquido. Tomo como para baixo.
Queda livre implica: .
é positivo, substitua-o pela velocidade .
Passo 2
- Assim, para encontrarmos a expressão para a velocidade do liquido em função da distancia y de sua queda partimos da equação:
- Temos que
Que nos dá
E
A equação da continuidade nos diz que
E como , isso se torna
E
E então usaremos isso acima para eliminar
Para corresponder à notação no problema, deixe e , pois o ponto 1 é onde o líquido sai primeiro no tubo e deixe ser e ser .
A equação que derivamos se torna então
Passo 3
Queremos o valor de y que dá
Ou
O resultado obtido na parte (a) diz
A equação derivada na parte (a) diz que r diminui com a distância abaixo da extremidade do tubo.