Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.7 - Ex. 16
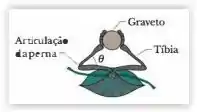
Alguns insetos podem se deslocar pendurados em gravetos. Suponha que um desses insetos tenha massa m e esteja pendurado em um graveto horizontal, como mostra a Fig. 5-35, com um ângulo . As seis pernas do inseto estão sob a mesma tensão e asseções das pernas mais próximas do corpo são horizontais. (a) Qual é a razão entre a tensão em cada tíbia (extremidade da perna) e o peso do inseto? (b) Se o inseto estica um pouco as pernas, a tensãonas t:Ibias aumenta, diminui ou continua a mesma?
Passo 1
Bom pessoal , o inseto tem seis pernas e a componente vertical da tração em cada perna , como podemos ver na imagem , é , sendo . Aplicando a Segunda Lei de Newton à componente vertical das forças envolvidas, vemos que, para que a aceleração seja zero na direção vertical, devemos ter :
O que nos dá :
Passo 2
Como o ângulo é medido em relação à horizontal, quando o inseto “estica as pernas” o ângulo aumenta (se aproxima de ), o que faz aumentar (se aproximar de); em consequência, diminui , como vimos na fórmula achada no item anterior.
Tranquilo galera??? Bora resolver mais questões então
Resposta
Ei, a resposta está no passo a passo :)