Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.7 - Ex. 15
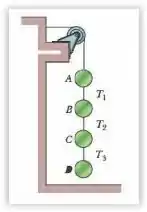
A Fig. 5-33 mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas (a) do disco , (b) do disco, (c) do disco C e (d) do disco?
Passo 1
Vamos começar pelo disco D. Nela atuam a força peso e em sentidos contrários.
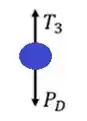
Como o somatório das forças é igual a zero podemos obter a seguinte equação:
Com isso podemos substituir os valores na equação para obter a massa do disco D:
Passo 2
Agora vamos para o disco C. As forças que atuam sobre ele são:
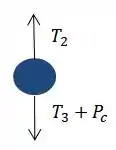
Novamente pelo somatório das forças igual a zero, podemos obter a seguinte equação :
Vamos substituir os valores que já temos na equação para obter a massa do disco C:
Passo 3
Vamos analisar as forças que atuam em B.
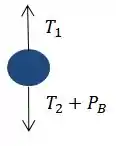
Como o somatório das forças é igual a zero podemos obter a seguinte equação:
Substituindo os valores que sabemos na equação para obter a massa do disco B:
Passo 4
Agora só falta o disco A.
Vamos analisar as forças:
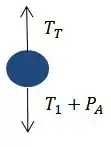
Sabendo que a força exercida na parede vale , essa vai ser a nossa tração total que está sendo exercida, usando o somatório de forças igual a zero teremos:
Substituindo os valores que sabemos na equação para obter a massa do disco A:
De boa pessoal?? Então partiu fazer mais exercícios!!!
Resposta
Ei, a resposta está no passo a passo :)