Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 33

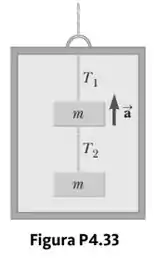
Dois blocos, cada um com massa de m   =   3,50   k g , estão pendurados no teto de um elevador como na Figura P4.33.

  1. Se o elevador se move com uma aceleração para cima   a → de módulo 1,60   m / s 2 , encontre as tensões T 1 e T 2 nas cordas superior e inferiores.
  2. Se as cordas puderem suportar uma tensão máxima de 85,0   N , qual é a aceleração máxima que o elevador tem antes de uma corda se romper?

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo e bora!

Letra a:

Observe que cada bloco experimenta uma força de gravidade para baixo:

F s = 3.50 k g 9.80 m s 2 = 34.3 N

Além disso, cada um tem a mesma aceleração para cima como o elevador, neste caso a y = + 1.60 m / s 2 .

Aplicando a segunda lei de Newton ao bloco inferior:

Σ F y = m a y ⇒ T 2 - F g = m a y

T 2 = F g + m a y = 34.3 N + 3.50 k g 1.60 m s 2 = 39.9 N

Em seguida, aplicando a segunda lei de Newton ao bloco superior:

Σ F y = m a y ⇒ T 1 - T 2 - F g = m a y

T 1 = T 2 + F s + m a y = 39.9 N + 34.3 N + ( 3.50 k g ) 1.60 m s 2 = 79.8 N

Passo 2

Letra b:

Observe que a tensão é maior na corda superior, e esta corda irá quebrar primeiro, à medida que a aceleração do sistema aumenta. Portanto, desejamos encontrar o valor de a y , quando T 1 = 85.0 .

Fazendo uso das relações gerais usadas em (a) acima, temos:

T 1 = T 2 + F g + m a y = F s + m a y + F g + m a y = 2 F g + 2 m a y

a y = T 1 - 2 F s 2 m = 85.0 N - 2 34.3 N 2 3.50 k g = 2.34 m s 2

Resposta

  1. 79.8 N
  2. 2.34 m s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um quadro está suspenso em uma parede por dois fios ligados em seus cantos superiores. Se os dois fios fazem o mesmo ângulo com a vertical, qual deve ser o ângulo se a tensão em cada fio for igual a 0
Um arqueólogo aventureiro passa de um rochedo para outro deslocando-se lentamente com as mãos por meio de uma corda esticada entre os rochedos. Ele para e fica em repouso no meio da corda (Figura 5.42
Uma bola grande de um guindaste de demolição é mantida em equilíbrio por dois cabos de aço leves (Figura 5.43 ). Se a massa m da bola for igual a 4090 k g , qual é a) a tensão T B no cabo que faz um â
Ache a tensão em cada corda na Figura 5.44 , sabendo que o peso suspenso é p .
Em quase todos os problemas deste livro, as massas dos cabos, cordas e fios são tão pequenas em comparação com os outros corpos que podemos desprezá-las. Porém, quando a corda é o único objeto do prob