Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 8.Problemas - Ex. 91

Os amigos Beto e Ernesto estão parados em extremidades opostas de um tronco uniforme flutuando em um lago. O tronco tem 3,0   m de extensão e massa de 20,0   k g . Beto tem massa de 30,0   k g e Ernesto, de 40,0   k g . Inicialmente, o tronco e os dois amigos estão em repouso em relação à margem. Então Beto oferece um biscoito a Ernesto, e Ernesto caminha até a extremidade de Beto no tronco para apanhá-lo. Em relação à margem, que distância o tronco se moveu quando Ernesto alcançou Beto? Ignore qualquer força horizontal que a água exerça sobre o tronco e considere que nenhum dos dois amigos cai do tronco

Passo 1

Fala pessoal, beleza?

Para resolver esse problema vamos apenas uma coisinha: o centro de massa do sistema deve permanecer em repouso ao longo do movimento!

Considere a representação do problema feita a seguir comparando a situação inicial com Ernesto (massa m 1 = 40,0   k g ) na extremidade esquerda e Beto (massa m 2 = 30,0   k g ) na extremidade direita. Na situação final, ambos estão na extremidade direita e o tronco (de massa M = 20,0   k g e comprimento L = 3,0   m ) se deslocou x para esquerda:

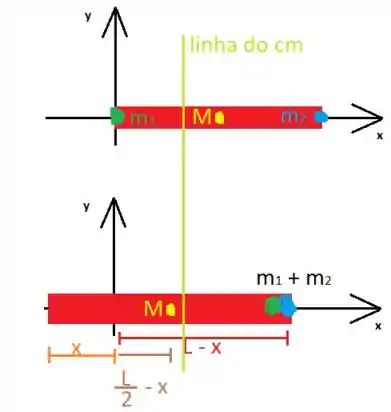
Repare que desenhei a linha que representa o centro de massa do sistema, que não deve se mover!

Passo 2

Na situação inicial, a posição do centro de massa é dada por

x c m = m 1 ⋅ 0 + M ⋅ L 2 + m 2 ⋅ L m 1 + M + m 2

Já na situação final, temos que

x c m = M ⋅ L 2 - x + m 1 + m 2 ⋅ L - x m 1 + M + m 2

Igualando as duas expressões, temos que

M ⋅ L 2 + m 2 ⋅ L = M ⋅ L 2 - x + m 1 + m 2 ⋅ L - x

Passo 3

Agora é só substituir as massas e resolver a equação para achar x :

20,0 ⋅ 3,0 2 + 30,0 ⋅ 3,0 = 20,0 ⋅ 3,0 2 - x + 30,0 + 40,0 ⋅ ( 3,0 - x )

Assim,

30 + 90 = 30 - 20 x + 210 - 70 x

Logo,

90 x = 210 - 90

Portanto,

x = 120 90

Com isso, achamos

x = 1,33   m

Resposta

x = 1,33   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você lança um bumerangue, por um tempo, ele "voa" horizontalmente em linha reta com rapidez constante, ao mesmo tempo que girando rapidamente em torno de si próprio. Desenhe uma série de figuras, com
Dê um exemplo para cada caso seguinte: (a) um objeto tridimensional sem matéria em seu centro de massa, (b) um objeto sólido cujo centro de massa está fora dele, (c) uma esfera sólida cujo centro de m
APLICAÇÃO BIOLÓGICA. Quando você está de pé, seu centro de massa está localizado dentro do volume do seu corpo. No entanto, se você se curva (como para levantar um pacote), a localização do centro de
APLICAÇÃO EM ENGENHARIA. Em sua viagem (de ida) de três dias até a Lua, a equipe Apollo (final dos anos de 1960 a início dos anos de 1970) separava de forma explosiva o módulo lunar do terceiro estági
Uma placa circular de raio R tem, cortado, um furo circular de raio R / 2 (Figura abaixo). Encontre o centro de massa da placa depois de o furo ter sido cortado. Dica: A placa pode ser vista como dois