Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 136
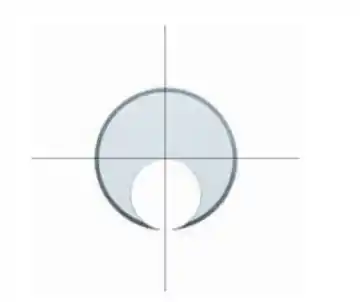
Uma placa circular de raio tem, cortado, um furo circular de raio (Figura abaixo). Encontre o centro de massa da placa depois de o furo ter sido cortado. Dica: A placa pode ser vista como dois discos superpostos, o furo representando um disco de massa negativa.
Passo 1
Por simetria, . Seja a massa por unidade de área do disco. A massa do disco modificado é a diferença entre a massa do disco todo e a massa do disco que foi removida.
Passo 2
Começando com a definição de :
A massa completa do disco é:
E a massa do material removido:
Passo 3
Então, substituindo e simplificando, obtemos:
Resposta
Exercícios de Livros Relacionados
Determine a posição do centro de massa do sistema constituído pelo Sol e por Júpiter. (Como a massa de Júpiter é muito maior do que as massas dos demais planetas, esta resposta fornece essencialmente
Um modelo de avião com controle remoto possui momento linear dado por: [ ( - 0,75k g m s ³ ) t ²+ ( 3,0k g m s ) ] î+ ( 0,25k g m s ² ) t j ³ ² î ² a) Quais são os componentes x, y e z da força result
As massas e as coordenadas dos centros de massa de três blocos de chocolate são dadas por: (1)0,300 kg, (0,200 m, 0,300 m): (2)0,400 kg, (0,100 m, -0,400 m), (3)0,200 kg, (-0,300 m, 0,600 m). Calcule
Uma jovem de 45,0 kg está em pé sobre uma canoa de 60,0 kg e comprimento igual a 5,00 m . Ela caminha a partir de um ponto situado a 1,00 m de uma das extremidades da canoa até atingir a outra extremi
Os objetos da Figura 8.41 foram feitos com aramesuniformes e dobrados nas formas indicadas. Ache a posição docentro de massa de cada um destes objetos .