Exercícios de Posição do Centro de Massa - Lista de Exercícios Resolvida
Questão 1
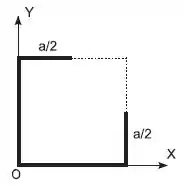
Um arame homogêneo e uniforme, de espessura desprezível, é moldado na forma de um quadrado de aresta Retira-se então um segmento de comprimento de duas arestas , reduzindo-as à metade, como mostra a figura. No novo sistema a distância do centro de massa à origem é igual a,
Ver solução completa
Questão 2
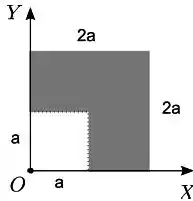
Uma chapa homogênea quadrada de lado tem um canto quadrado de lado retirado. A chapa restante está disposta no plano como indicado na figura. Em relação à origem , o vetor posição do centro de massa
Ver solução completa
Questão 3
Encontre a posição do centro de massa da chapa abaixo, considere a chapa homogênea.
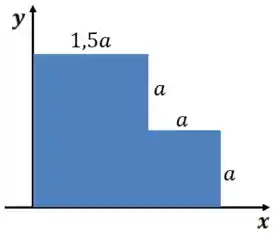
Questão 4
Calcule o centro de massa do objeto esquematizado na figura abaixo (despreze a massa da grade):
Questão 5
Encontre a posição do centro de massa da chapa abaixo de raio , sabendo que foi feito um furo dela de raio posicionado como indicado na figura. Considere também que a chapa é homogênea.
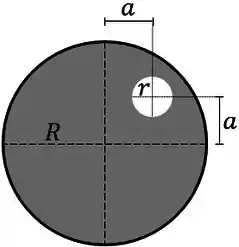
Questão 6
Encontre a posição do centro de massa do objeto desenhado na figura abaixo, sabendo que ele é constituído por 6 pedações de arames homogêneo feitos do mesmo material.
Questão 7
Considere a molécula d’água com seus três átomos distribuídos com localizações fixas de acordo com a figura abaixo, sendo a distância entre o átomo de Oxigênio e um átomo de Hidrogênio . Encontre o vetor posição do centro de massa da molécula, em relação à posição do átomo de Oxigênio, em função da distância .
Sabe-se que , , , e (unidades de massa atômica).
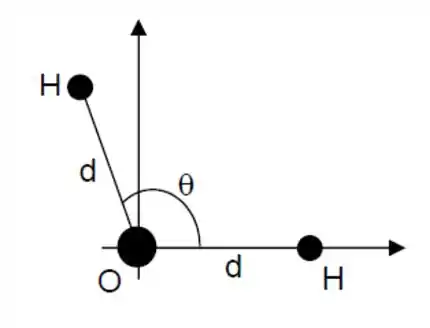
Questão 8
Uma barra de comprimento é formada por duas metades, como mostra a figura. A parte da esquerda possui metade da massa da parte da direita, hachurada. Separadamente, as duas partes são homogêneas. Desejamos usar um fio para prender esta barra ao teto. Para que a barra fique em equilíbrio, na posição horizontal, ela deve ser pendurada pelo ponto tal que
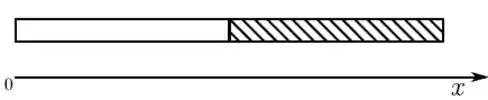
(a)
(b)
(c)
(d) seja qualquer entre e
(e) seja qualquer entre e
Ver solução completaQuestão 9
Uma barra de comprimento é formada por duas metades, como mostra a figura. A parte da esquerda possui metade da massa da parte da direita, hachurada. Separadamente, as duas partes são homogêneas. Desejamos usar um fio para prender esta barra ao teto. Para que a barra fique em equilíbrio, na posição horizontal, ela deve ser pendurada pelo ponto tal que
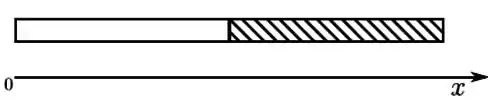
(a)
(b)
(c)
(d) seja qualquer entre e
(e) seja qualquer entre e
Ver solução completaQuestão 10
Quatro contas estão presas nos vértices de um arame quadrado de lado , como mostra a figura. Duas contas possuem massa e as outras duas massa . Desprezando a massa do arame e de acordo com o sistema de referência indicado na figura, a posição do centro de massa do arranjo é:
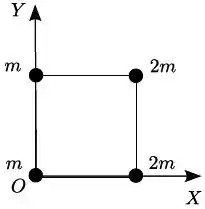
- e ;
- e ;
- e ;
- e ;
- e ;
Questão 11
Um projétil é lançado de uma plataforma do ponto e num dado instante após ser lançado ele se fragmenta em dois pedações de massa e , que caem simultaneamente nas posições horizontais e respectivamente. Se o projétil não se fragmentasse o seu alcance seria,
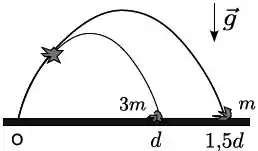
- ;
- ;
- ;
- ;
- ;
Questão 12
Uma chapa homogênea quadrada de lado tem um canto quadrado de lado retirado. A chapa restante está disposta no plano como indicado na figura. Em relação à origem , o vetor posição do centro de massa
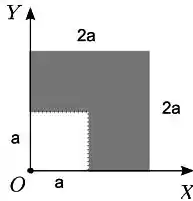
Questão 13
Vamos supor que duas partículas e colidem bidimensionalmente. Seja a partícula de massa e a partícula de massa . As posições das partículas num certo instante antes da colisão são dadas por e . O tempo de duração da colisão é de .
a) Calcule o vetor de posição do centro de massa no instante .
b) Suponha agora que as velocidades no início da colisão são: e , e que no fim da colisão a componente da velocidade de é igual a e a componente da velocidade de é . Escreva os vetores velocidade de ambas as partículas no fim da colisão.
c) Suponha agora que as velocidades no início da colisão são: e , e que a colisão é completamente inelástica. Calcule o vetor força média que atua na partícula durante a colisão ().
Ver solução completaQuestão 14
Considere a molécula d’água com seus três átomos distribuídos com localizações fixas de acordo com a figura abaixo, sendo a distância entre o átomo de Oxigênio (O) e um átomo de Hidrogênio (H). Encontre o vetor posição do centro de massa da molécula, em relação à posição do átomo de Oxigênio, em função da distância .
Sabe-se que , , , e (unidades de massa atômica).
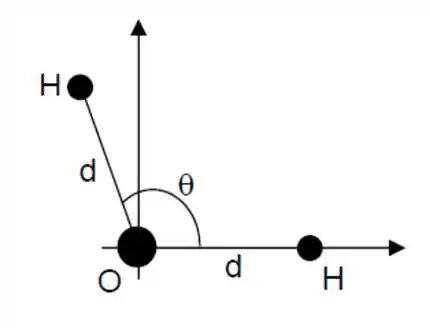
Questão 15
Um corpo de massa desliza sem atrito ao longo do eixo horizontal , com velocidade , até colidir elástica e instantaneamente com outro corpo, de massa , que está em repouso.
a) Calcule as velocidades e dos corpos 1 e 2 após a colisão.
Após a colisão entre 1 e 2, o corpo 2 colide com o corpo 3 em repouso, de massa , de modo que a colisão é completamente inelástica.
b) Calcule as velocidades finais e após esta segunda colisão.
c) Calcule a velocidade final do CM do sistema formado pelos corpos 2 e 3 e a percentagem da energia mecânica inicial que foi dissipada na colisão.
Para o próximo item volte à situação do item mas suponha que agora existe uma mola em sua forma relaxada ligando o corpo 2 ao corpo 3. A colisão entre 1 e 2 é novamente instantânea e elástica.
d) Calcule as velocidades e dos corpos 1 e 2 após a colisão nesta nova situação usando os mesmos dados que para o item .
Ver solução completaQuestão 16
Um sistema é constituído de três partículas de mesma massa localizadas nos semi-eixos positivos , e a uma mesma distância da origem, como indica a figura. O vetor posição do centro de massa do sistema é
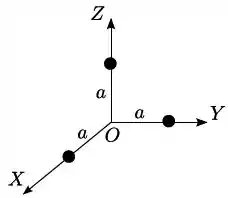
- ;
- ;
- ;
- ;
- ;
Questão 17
Uma massa de pizza perfeitamente circular e homogênea tem raio e massa. Se retirarmos dela pedaço perfeitamente circular com diâmetro de modo que a massa que resta tem a forma da figura, podemos afirmar que o centro de massa do que restou:
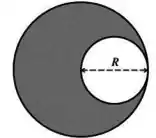
- Se deslocou uma distância para a esquerda do centro de massa original.
- Se deslocou uma distância para a direita do centro de massa original.
- Se deslocou uma distância para a esquerda do centro de massa original.
- Se deslocou uma distância R/2 para a direita do centro de massa original.
- Está na mesma posição do centro de massa original.
Questão 18
8) Um carro com tração nas quatro todas realiza uma curva plana circular e, durante todo o movimento, mantém o módulo de sua velocidade constante e não derrapa em nenhum momento. Considere que o atrito é igual nas quatro rodas. Sobre a força de atrito realizada pelo solo sobre uma das rodas do carro, é correto afirmar que:
(a) a força resultante sobre o carro é nula, já que sua velocidade é constante.
(b) é uma força de atrito estático responsável por impedir que o carro derrape, isto é, por impedir que o carro deslize lateralmente, saindo do traçado da curva.
(c) é uma força de atrito cinético perpendicular à trajetória do veículo
(d) é uma força de atrito estático que se opõe ao movimento do veículo sem alterar a sua velocidade
(e) é uma força de atrito cinético, já que o carro está em movimento com relação ao solo.
Ver solução completaQuestão 19
No tempo inicial , uma partícula A de massa parte da posição e move-se em movimento retilíneo uniforme (MRU) com velocidade . No mesmo instante, uma partícula B de massa parte do repouso da posição e move-se em movimento retilíneo uniformemente variado (MRUV) com aceleração . Determine o vetor posição do centro de massa deste sistema de duas partículas no instante .
Ver solução completaQuestão 20
Um sistema massa-mola consiste de uma partícula de massa presa a uma mola de constante elástica e massa desprezível. Montamos este sistema sobre uma plataforma móvel de massa conforme mostrado na figura. A posição de equilíbrio coincide com centro de plataforma, conforme mostra a figura , e tanto a massa se desloca sem atrito sobre a plataforma, quanto a plataforma se desloca sem atrito sobre a superfície horizontal. Suponhamos que a mola seja distendida em e solta, com o sistema todo inicialmente em repouso.
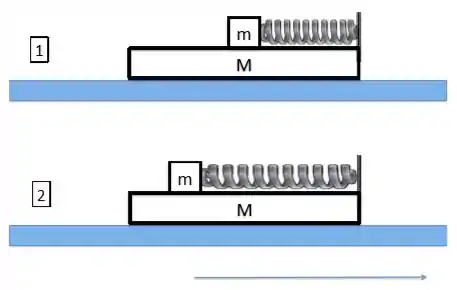
O deslocamento da plataforma, quando a mola estiver comprimida em ,
A velocidade (módulo e sentido) do bloco de massa nesta condição.
A velocidade (módulo e sentido) da plataforma nesta condição.
Ver solução completaQuestão 21
Uma bolinha de raio desprezível e massa , é colocada na borda de um disco de raio e massa . A que distância do centro do disco encontra-se o Centro de Massa desta configuração?
Questão 22
Uma corrente é mantida sobre uma mesa sem atrito, com de seu comprimento pendurado fora da mesa, conforme a figura abaixo. Se a corrente tem comprimento e massa , qual o trabalho necessário para puxá-la totalmente para cima da mesa?

a)
b)
c)
d)
e)
Ver solução completaQuestão 23
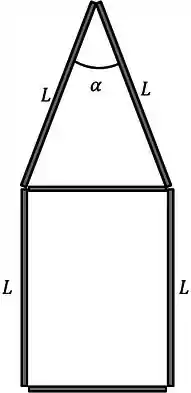
A figura ao lado mostra um sistema formado por três hastes retilíneas, cada uma de comprimento e massa , conectadas em forma de e uma chapa quadrada (região hachurada), de aresta e massa . Considere que as espessuras das hastes e da chapa são iguais e muito menores do que . Assinale a alternativa que corretamente expressa a posição do centro de massa do sistema (hastes + chapa):
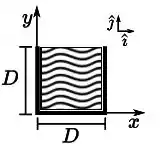
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 24
Um dado viciado é construído com uma das suas faces mais pesada que as demais. Suponha que em um dado destes, faces tem massa , e a sexta face tem massa . A aresta do dado tem . A que distância da face mais pesada encontra-se o centro de massa?
a)
b)
c)
d)
e)
Ver solução completaQuestão 25
Considere um sistema formado por duas pequenas esferas de massas e , ligadas por uma mola ideal. Inicialmente, a mola é comprimida e o sistema é lançado, liberando a mola, de uma certa altura acima do solo, com o centro de massa tendo velocidade na direção horizontal e as esferas tendo uma velocidade angular , em relação à posição do centro de massa. Sobre o movimento que se segue é correto afirmar que:
(a) A posição do centro de massa do sistema descreverá uma trajetória parabólica, de um projétil.
(b) As esferas executarão um movimento circular uniforme em torno da posição do centro de massa, de velocidade angular .
(c) Ambas as esferas vão descrever um movimento parabólico, de projétil.
(d) A esfera de massa vai realizar um movimento circular uniforme em torno da esfera de massa .
(e) No instante imediatamente anterior ao sistema atingir o solo, necessariamente a esfera de massa terá uma velocidade angular em torno da posição do centro de massa de , onde é a distância entre a esfera e a posição do CM.
Ver solução completaQuestão 26
Na molécula de amônia () da fogira mostrada a seguir, três átomos de hidrogênio (H) formam um triângulo equilátero, com o centro do triângulo a uma distância de cada átomo de hidrogênio. O átomo de nitrogênio (N) está no vértice superior de uma pirâmide, com os três átomos de hidrogênio formando a base. A razão entre as massas de nitrogênio e do hidrogênio é e a distância nitrogênio-hidrogênio é . Quais são as coordenadas
(a) e
(b) do centro de massa da molécula?
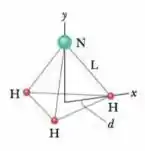
Questão 27
Uma chapa metálica de densidade superficial uniforme (I) pode ser cortada das formas (II) ou (III):

Considerando sistemas de coordenadas no centro de cada forma e orientadas como o da figura, é correto afirmar que a posição do CM das figuras obedeca a:
- ,
- ,
- ,
- ,
- ,
Questão 28
Um sistema é formado por 4 partículas que se encontram nos vértices de um quadrado de lado , conforme mostra a figura.
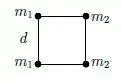
Sabendo que , qual a situação que representa a posição do centro de massa do sistema?
Questão 29
Uma haste homogênea muito fina de massa e de comprimento pode girar livremente num plano vertical, em torno de um pino que atravessa a haste a uma distância de uma de suas extremidades. A haste, que se encontrava inicialmente na posição vertical, com seu centro de massa acima do pino, é posta a girar no sentido horário, a partir do repouso. O trabalho do peso sobre a haste entre o instante inicial e o instante em que a haste passa pela posição horizontal é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 30
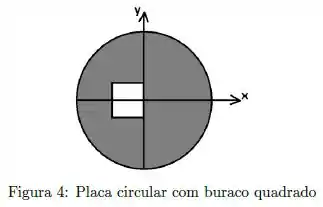
Considere a placa circular de densidade uniforme, de raio , com um buraco quadrado de lado , conforme mostrado na figura 4. Em coordenadas de acordo com os eixos e da figura, onde está localizado o centro de massa da placa?
(A) ; e
(B) ; e
(C) ; e
(D) ; e
(E) ; e
Ver solução completaQuestão 31
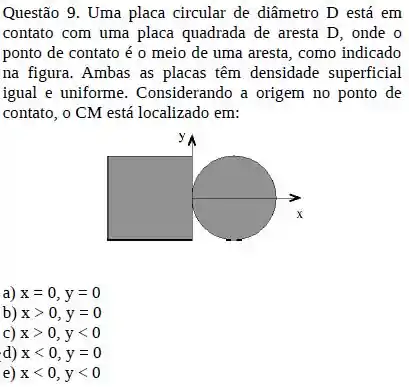
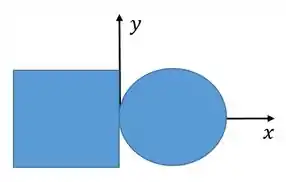
Considere o sistema formado por duas placas, uma circular de diâmetro , e outra quadrada de lado . O ponto de contato entre as placas é meio da aresta como indicado na figura, e a origem do sistema é definido nesse ponto. Se ambas as placas têm a densidade superficial igual e uniforme, as coordenadas do ponto de centro de massa (CM) do sistema é dado por:
a) e
b) e
c) e
d) e
e) e
Questão 32
Três massas puntiformes estão localizadas nos vértices de um triângulo equilátero de lado conforme mostra a figura abaixo. Considere as seguintes situações:
as três massas são idênticas e .
Sejam e as coordenadas do centro de massa desse sistema nas situações e , respectivamente, no referencial da figura. Sobre as coordenadas do centro de massa, podemos então afirmar que:
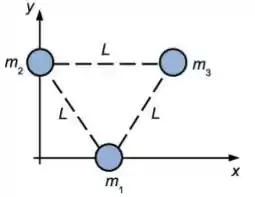
Ver solução completa
Questão 33
O centro de massa de uma barra não uniforme de tamanho e massa total está localizado à de uma das extremidades. Se grudarmos na extremidade oposta um objeto pontual de massa , de quanto se deslocará o centro de massa desta configuração?
- Depende do valor de
Questão 35
Um arame homogêneo e uniforme, de espessura desprezível, é moldado na forma de um quadrado de aresta Retira-se então um segmento de comprimento de duas arestas , reduzindo-as à metade, como mostra a figura. No novo sistema a distancia do centro de massa à origem é igual a,
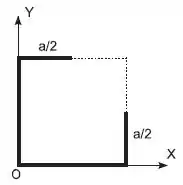
Questão 36
Duas massas pontuais estão colocadas no mesmo plano. A distância da massa ao centro de massa é . A distância da massa ao centro de massa é . Qual é a razão da massa para a massa ?
Ver solução completa
Questão 37
Considere uma colisão perfeitamente inelástica entre dois automóveis de mesma altura e mesmo comprimento . O automóvel tem massa e velocidade de módulo imediatamente antes de colidir com o automóvel que tem massa e está em repouso. A colisão se dá em um intervalo de tempo muito curto. Considere o sistema de coordenadas indicado na figura. Assuma que o centro de massa de cada automóvel está à meia altura e na metade de seu comprimento.
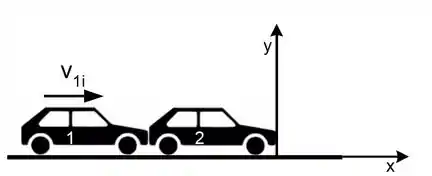
Determine o vetor posição do centro de massa do sistema (dois automóveis) no instante imediatamente antes da colisão.
Determine o vetor velocidade dos destroços imediatamente depois da colisão.
Encontre a expressão literal para a perda de energia cinética durante a colisão. Analise o resultado se .
Ver solução completaQuestão 38
Em uma barra uniforme de comprimento e massa , fixa-se uma partícula de massa em uma das extremidades, e outra massa na outra extremidade. O centro de massa desta distribuição encontra-se a que distância da partícula de massa ?
Ver solução completa
Questão 39
(Cap 5 – Ex 104) Por simetria, localize o centro de massa de uma folha uniforme em forma de triângulo equilátero com lados de comprimento . O triângulo tem um vértice no eixo e os outros em e .
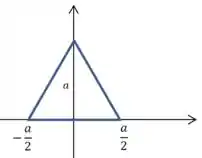
Questão 42
Dois tijolos homogêneos, de massas M e de comprimentos L, estão empilhados sobre o canto de uma mesa, um sobre o outro, como na figura ilustrativa abaixo. Quais são os maiores comprimentos possíveis a1 e a2 para que a pilha permaneça em equilíbrio?
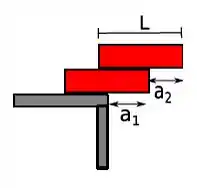
a) a1 = L/4; a2 = 2L/3
b) a1 = L/4; a2 = L/2
c) a1 = L/2; a2 = 3L/4
d) a1 = 4L/3; a2 = L/2
e) a1 = L/3; a2 = 4L/5
f) a1 = 5L/2; a2 = L/2
g) a1 = L/2; a2 = 2L/3
h) a1 = L/2; a2 = L/3
Ver solução completaQuestão 43
Dois patinadores, um de e outro de , estão em uma pista de gelo e seguram as extremidades de uma base de de comprimento e massa desprezível. Os patinadores se puxam ao longo da haste até se encontrarem. Qual é a distância percorrida pelo patinador de ?
Ver solução completaQuestão 44
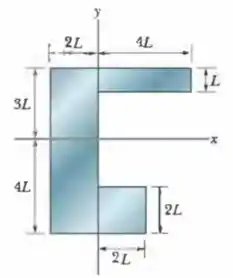
Quais são (a) a coordenada e (b) a coordenada do centro de massa da placa homogênea da Fig. 9-38 se ?
Questão 45
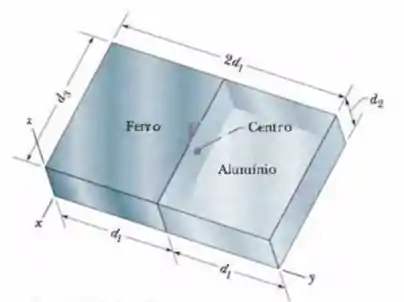
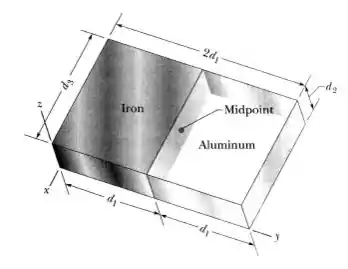
A Fig. 9-36 mostra uma placa composta de dimensões , e . Metade da placa é feita de alumínio (massa especifica = ) e a outra metade de ferro (massa especifica = ). Determine (a) a coordenada , (b) a coordenada e (c) a coordenada do centro de massa da placa.
Questão 46
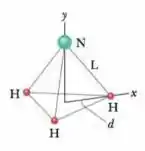
Na molécula de amônia () da Fig. 9-40, três átomos de hidrogênio (H) formam um triângulo equilátero, com o centro do triângulo a uma distância de cada átomo de hidrogênio. O átomo de nitrogênio (N) está no vértice superior de uma pirâmide, com os três átomos de hidrogênio formando a base. A razão entre as massas de nitrogênio e do hidrogênio é e a distância nitrogênio-hidrogênio é . Quais são as coordenadas (a) e (b) do centro de massa da molécula?
Questão 47
Uma lata tem uma massa de , uma altura de e contém de refrigerante (Fig. 9-42). Pequenos furos são feitos na base e na tampa (com perda de massa desprezível) para drenar o refrigerante. Qual é a altura do centro de massa da lata e seu conteúdo (a) inicialmente e (b) após a lata perder todo o refrigerante? (c) O que acontece com enquanto o refrigerante está sendo drenado? (d) Se é a altura do refrigerante que ainda resta na lata em um dado instante, determine o valor de no instante em que o centro de massa atinge o ponto mais baixo.

Questão 48
. Uma moça está parada no extremo direito de uma plataforma plana, que, por sua vez, também se encontra em repouso com relação à superfície de gelo em que se apoia. A moça, então, começa a correr para a esquerda com velocidade constante em relação à plataforma. Não há atrito entre a plataforma e a superfície de gelo, a massa da moça é , a massa da plataforma é e o tamanho da plataforma é . Tome a posição inicial do extremo esquerdo da plataforma em como mostrado na figura. Encontre o centro de massa do sistema (moça-plataforma) antes da moça começar a se mover. Quando a moça chega no extremo esquerdo da plataforma, esta se moveu uma distância (como na figura) determine .
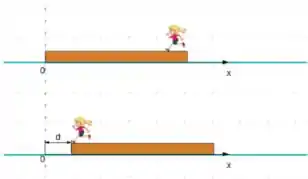
Questão 49
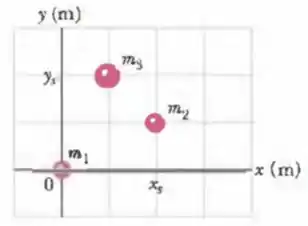
A Fig. 9-35 mostra um sistema de três partículas de massas , e . As escalas do gráfico são definidas por e . Quais são (a) a coordenada e (b) a coordenada do centro de massa do sistema? (c) Se aumenta gradualmente, o centro de massa do sistema se aproxima de , se afasta de ou permanece onde está?
Questão 50
Uma partícula de tem coordenadas (, ) e uma partícula de tem coordenadas (, ). Ambas estão em um plano horizontal. Em que coordenada (a) e (b) deve ser posicionada uma terceira partícula de para que o centro de massa do sistema de três partículas tenha coordenadas (, )?
Ver solução completaQuestão 51
A figura a seguir mostra uma placa composta de dimensões , e . Metade da placa é constituída de alumínio (densidade = ) e a outra metade de ferro (densidade = ). Quais são:
(a) a coordenada ,
(b) a coordenada e
(c) a coordenada do centro de massa da placa?
Questão 52
Um disco de massa e diâmetro e uma corda de massa desprezível e comprimento formam um pêndulo simples, que pode girar sem atrito em torno da origem do sistema de coordenadas ilustrado na figura. O pêndulo é largado do repouso a partir da horizontal. Quando o pêndulo está em sua posição mais baixa, como ilustrado em pontilhado na figura, ele colide com um bloco quadrado de lado e mesma massa, que está em repouso sobre uma superfície horizontal áspera. O coeficiente de atrito cinético entre o bloco e a superfície vale . A colisão ocorre durante o intervalo de tempo de um centésimo de segundo.
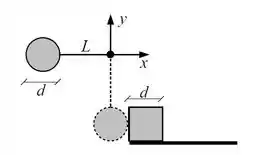
a) Calcule a posição do centro de massa do sistema (disco e bloco) imediatamente antes da colisão.
b) Sabendo que o pêndulo fica parado imediatamente após a colisão, calcule a velocidade do bloco para este instante de tempo.
c)Calcule a força média que o bloco faz no pêndulo durante a colisão.
d) Calcule distância percorrida pelo bloco até parar.
Ver solução completaQuestão 53
A figura ao lado representa o gráfico da velocidade por tempo para dois objetos, e , de massas e , respectivamente, que se movem em linha reta num trilho de atrito desprezível, antes e após eles colidirem entre si. O objeto B está inicialmente em repouso.
- Determine a velocidade do centro de massa do sistema antes e após a colisão.
-
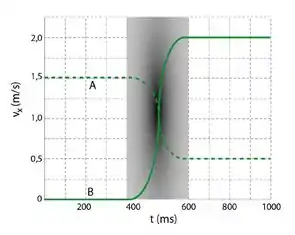
A sobre o objeto durante a colisão.
Questão 54
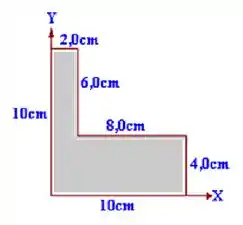
Calcule a partir da origem do sistema de coordenadas, as coordenadas do centro de massa da placa homogênea abaixo:
Questão 55
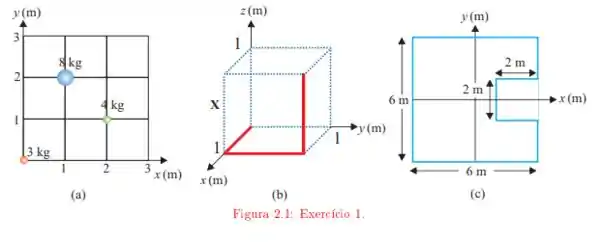
Ache as coordenadas do centro de massa das figuras seguintes. Em considere que os fios tem a mesma densidade linear de massa uniforme. Em considere que a densidade superficial de massa é uniforme.
Questão 56
Três pequenas esferas, , e , com as massas de , e , respectivamente, estão montadas nos vértices de um triângulo de hastes rígidas, muito leves. As coordenadas das esferas no plano são: , e .
a) Desenhe o sistema no plano ;
b) Que coordenada tem o centro de massa? Indique a posição do centro de massa no desenho da letra a).
Ver solução completaQuestão 57
A massa da folha de compensado é de . Qual a localização do centro de massa? Faça um desenho indicando a posição calculada.

Questão 58
Um taco de beisebol tem comprimento e a densidade linear de massa é dada por . Localizar a coordenada do centro de massa em termos de .
Ver solução completaQuestão 59
Calcule as coordenadas (xcm, ycm) do centro de massa do sistema de partículas da questão 17. Considere o ponto O como sendo a origem do sistema de coordenadas (x,y).
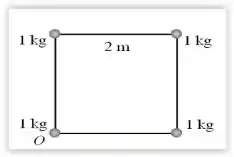
(A) (1,0m, 1,0m)
(B) (1,0m, 1,5m)
(C) (1,5m, 1,5m)
(D) (1,5m, 0)
(E) (1,5m, 1,0m)
Ver solução completaQuestão 60
Três partículas de massas e estão nas posições e . A posição do centro de massa constituído pelas três partículas está na posição:
Escolha uma:
- Não é possível calcular com os dados fornecidos
- Nenhuma das alternativas
Questão 61
O centro de massa de um sistema de partículas tem velocidade constante se:
A. a soma das forças externas que agem sobre as partículas do sistema é zero;
B. a soma das forças que as partículas exercem umas sobre as outras é zero;
C. a velocidade do centro de massa é inicialmente zero;
D. as partículas estão distribuídas simetricamente me torno do centro de massa;
E. o centro de massa está no centro geométrico do sistema;
Ver solução completaQuestão 62
Um reservatório de massa total M pode ser representado por uma caixa cúbica, oca, de paredes finas e homogêneas de lado L. O reservatório está parcialmente cheio por um líquido de densidade volumétrica uniforme ρ. Sabendo que a coluna do líquido no interior do reservatório tem altura h, a altura do centro de massa do conjunto reservatório + líquido em relação à base do reservatório é:
Questão 63
Dois blocos, de massas e , movem-se sobre um plano horizontal sem atrito com vetores posição dados como função do tempo respectivamente por e, com todas as unidades no SI. (Se julgar necessário, utilize o par de eixos ao lado como auxílio.)
(a) Para o instante , encontre, em termos dos vetores unitários, o vetor posição do centro de massa.
Considerando que os blocos colidem de modo totalmente inelástico, calcule:
(b) o ângulo entre o vetor velocidade do conjunto e o semieixo positivo .
Considerando uma outra colisão em que o segundo bloco adquire velocidade final, calcule:
(c) o vetor velocidade final do primeiro bloco, em termos dos vetores unitários.
Ver solução completaQuestão 64
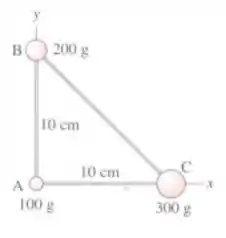
As três massas mostradas na figura estão conectadas por hastes rígidas de massas desprezíveis. Determine as coordenadas do centro de massa do sistema.
Questão 65
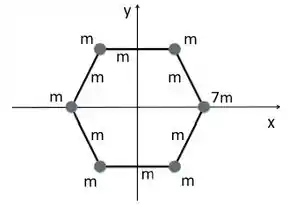
Um sistema hexagonal é formado por hastes idênticas, de massa , e tem por vértices cinco partículas de massa e uma partícula de massa . Encontre a posição (,) do CM desse sistema, sabendo que cada lado do hexágono uniforme vale e que seu centro se encontra em (,). Justifique sua resposta.
Questão 66
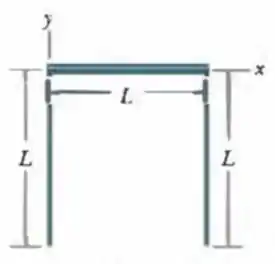
Na figura mostrada a seguir, três barras finas e uniformes, de comprimento , formam um invertido. Cada barra vertical tem uma massa de ; a barra horizontal tem massa de . Quais são
(a) a coordenada e
(b) a coordenada do centro de massa do sistema?
Questão 67
Dois patinadores, um de e outro de , estão em uma pista de gelo e seguram as extremidades de uma base de de comprimento e massa desprezível. Os patinadores se puxam ao longo da haste até se encontrarem. Qual é a distância percorrida pelo patinador de ?
Ver solução completaQuestão 68
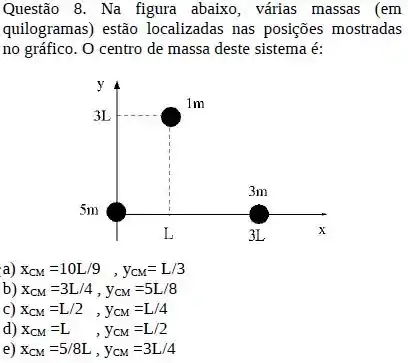
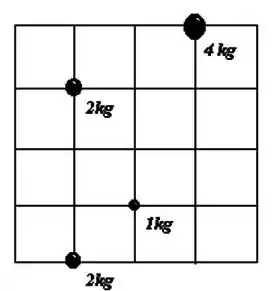
Na figura abaixo, várias massas (em quilogramas) estão localizadas nas posições mostradas no gráfico. O centro de massa deste sistema é:
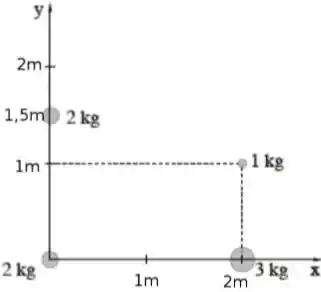
a) ,
b) ,
c) ,
d) ,
e) ,
Ver solução completa