Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 18.8 - Ex. 36
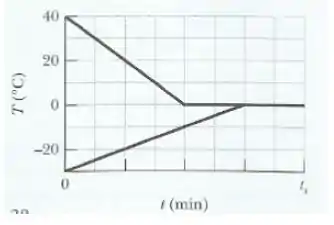
Uma amostra de de água e uma amostra de gelo são colocadas em um recipiente termicamente isolado. O recipiente também contém um dispositivo que transfere calor da água para o gelo a uma taxa constante até que o equilíbrio térmico seja estabelecido. As temperaturas da água e do gelo são mostradas na figura abaixo em função do tempo ; a escala do eixo horizontal é definida por .
Qual é a taxa ?
Qual é a massa inicial de gelo no recipiente?
Quando o equilíbrio térmico é atingido, qual é a massa do gelo produzido no processo?
Passo 1
Falaaaa galerinha, tudo belezinha? Vamos treinar mais um pouco de calorimetria? Bora lá...
Sabemos que a capacidade térmica é dada pela expressão:
Onde é o calor especifico, a massa enquanto é a variação de temperatura. Sendo assim, obtemos que:
E a malandragem é que como o enunciado nos diz que a taxa de transferência de calor é constante, sendo assim, através do gráfico temos que:
Logo:
Passo 2
Iradoso, agora na letra (b), durante o mesmo intervalo de do item (a), a temperatura do gelo aumenta . De acordo com a equação:
Temos que a massa será dada como:
Logo:
Passo 3
Já na letra (c), pra gente calcular a quantidade de gelo produzida no processo usamos a Tabela 18-4, e a equação do calor de transformação, dada como:
Logo:
MAAASSS, a malandragem agora é a notar que vamos usar apenas o calor relacionado ao tempo em que o gelo é produzido congelando a água que já está a , de forma que esse tempo equivale:
Sendo assim, o calor associado a esse tempo é:
Logo:
