Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 18.11 - Ex. 50

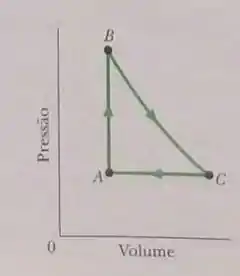
Um gás em uma câmara passa pelo ciclo mostrado na figura. Determine a energia transferida pelo sistema na forma de calor durante o processo se a energia adicionada como calor

durante o processo é , nenhuma energia é transferida como calor durante o processo e o trabalho realizado durante o ciclo é .

Passo 1

Primeiro, vamos lembrar da primeira lei da termodinâmica, aquela que relaciona a variação de energia interna e o trabalho realizado ao longo de um processo. Aplicando-a para o ciclo inteiro, a gente tem:

Como em um ciclo a variação de energia interna é sempre nula, temos:

Passo 2

Ok! Mas por que essa informação é importante?

Lembre que o calor transferido durante o ciclo todo é a soma dos trabalhos transferidos em cada etapa do ciclo. Daí, nesse caso, temos:

Então:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra um ciclo composto de cinco trajetórias: A B é isotérmica a 300K , B C é adiabática com um trabalho de 5,0J , C D é a uma pressão constante de 5a t m , D E é isotérmica e E A é adiabáti

Estime o rendimento máximo de um motor de automóvel que tenha uma razão de compressão de 8 : 1 . Suponha que a máquina opere no ciclo Otto, e que γ = 1.4 .

Uma amostra de 1 mol de gás N 2 , a 20°C e 5 atm, expande-se adiabaticamente até que sua pressão seja igual a 1 atm. Ele é, então, aquecido à pressão constante até que sua temperatura seja novamente 2

Uma amostra de 2 mol de um gás monoatômico ideal tem uma pressão inicial de 2 atm e um volume inicial de 2 L. O gás é, então, conduzido através do seguinte ciclo quase estático: Ele se expande isoterm

Uma amostra de 1 mol de gás diatômico se expande. Esta expansão é representada pela linha reta de 1 até 2 no diagrama PV (Figura 18-23). Depois, o gás é comprimido isotermicamente. Esta compressão é r