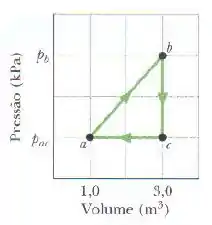
Uma amostra de um gás ideal é submetida ao processo cíclico abca mostrado na figura. A escala do eixo vertical é definida por e . No ponto , . (a) Quantos mols do gás estão presentes na amostra? Qual é (b) a temperatura do gás no ponto , (c) a temperatura do gás no ponto e (d) a energia adicionada ao gás na forma de calor ao ser completado o ciclo?

(b) Agora se queremos calcular a temperatura no ponto , vamos usar aquilo que quase sempre usamos quando vamos comparar dois pontos de uma transformação;

Sendo assim:

(c) Agora vamos fazer basicamente a mesma coisa que fizemos na letra (b), vamos comparar o ponto com o ponto :

Portanto:

(d) Agora queremos calcular qual foi a energia adicionada ao gás na forma de calor.

Bom, pela primeira lei da termodinâmica:

Mas em um ciclo completo, em que a gente volta pro mesmo ponto onde começamos, a variação de energia interna é zero, concorda?

Ou seja, o calor adicionado ao gás é igual ao trabalho realizado pelo gás. E sabemos calcular o trabalho:

Que a gente pode interpretar como sendo a área daquele triângulo retângulo no gráfico!

Pra calcular a área do retângulo, é só fazer o clássico “base vezes altura divido por dois”:

E então o calor é igual a isso, logo:

Pronto!