Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.2 - Ex. 23

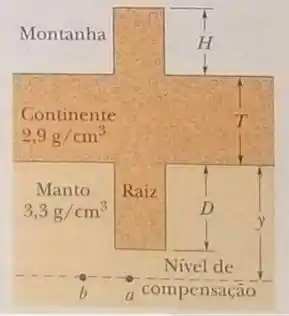
Na análise de certos fenômenos geológicos, é muitas vezes apropriado supor que a pressão em um dado nível de compensação horizontal, muito abaixo da superfície, é a mesma em uma vasta região e é igual à pressão produzida pelo peso das ·rochas que se encontram acima desse nível. Assim, a pressão no nível de compensação é dada pela mesma fórmula usada para calcular a pressão de um fluido. Esse modelo exige, entre outras coisas, que as montanhas tenham raízes de rochas continentais que penetram no manto mais denso (Fig. 14-34). Considere uma montanha de altura H   =   6,0   k m em um continente de espessura T   =   32   k m . As rochas continentais têm uma massa específica 2,9   g / c m ³ e o manto que fica abaixo destas rochas tem uma massa específica de 3,3   g / c m 3 . Calcule a profundidade D da raiz. (Sugestão: iguale as pressões nos pontos a e b ; a profundidade y do nível de compensação se cancela)

Passo 1

Fala galerinha do RespondeAí, tudo show de bolinhas?

Se liga só, nesse exercício aqui vamos utilizar o fato de que a pressão de um fluido em repouso varia (entre dois pontos 1 e 2 no interior de um fluido de densidade ρ ) de acordo com a posição vertical y do seguinte modo:

p 2 = p 1 + ρ g ( y 2 - y 1 )

Lembrando que, quando há dois fluidos que não se misturam superpostos, as contribuições de ambos devem ser contabilizadas no segundo elemento do membro direito, ou seja, devem ser somados os termos ρ 1 g y 2 - y 1 e ρ 2 g y 2 - y 1 .

Passo 2

Nesse caso, analisando o ponto B , temos:

p b = p a t m + ρ m a n t o g y + ρ c o n t i n e n t e g T

Já para o ponto A , temos:

p a = p a t m + ρ m a n t o g y - D + ρ c o n t i n e n t e g ( D + T + H )

Passo 3

Iradoso, agora a gente precisa lembrar que para um fluido em repouso, pontos localizados na mesma horizontal são submetidos a uma mesma pressão, temos:

p a = p b

Igualando as expressões de p a e p b , temos:

D = 6   km × ρ c o n t i n e n t e ρ m a n t o - ρ c o n t i n e n t e

D = 6   km × 2,9   g/cm³ 3,3   g/cm³ - 2,9 g/cm³

D = 44   km

Resposta

D = 44   km

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um copo de água, na vertical, acelera para a direita ao longo de uma superfície plana horizontal. Qual é a origem da força que produz a aceleração de um pequeno elemento de água no meio do copo? Expli
Plasma sanguíneo flui de uma bolsa, através de um tubo, para a veia de um paciente, onde a pressão sanguínea é 12 mmHg. A densidade do plasma sanguíneo a 37°C é 1,03. Qual é a menor elevação que a bol
Um curto-circuito elétrico impede o fornecimento d potencia necessária para um submarino que está situado a 30m abaixo da superfície do oceano, A tripulação deve empurrar uma escotilha com área de 0,7
Calcule a diferença na pressão sanguínea entre os pés e o topo da cabeça de uma pessoa de 1,56m de altura. (b) Considere um segmento cilíndrico de um vaso sanguíneo de 2,0cm de comprimento e 0,50mm de
Um lago no extremo norte do Yukon está oberto por uma camada de gelo de 1,75m de espessura. Calcule a pressão absoluta e a pressão manométrica a uma profundidade de 2,50m no lago.