Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.3 - Ex. 25

A coluna de um barômetro de mercúrio (como o da Fig.14-5a) tem uma altura h   =   740,35 mm. A temperatura é - 5,0   º C , na qual a massa específica do 1nercúrio é ρ   =   1,3608   x   10 4   k g / m ³ . A aceleração de queda livre no local onde se encontra o barômetro é g =   9,7835 m / s ² . Qual é a pressão atmosférica medida pelo barômetro em pascal e em torr (que é uma unidade muito usada para as leituras dos barômetros)?

Passo 1

Fala ai galerinha, tudo certo?!

A gente precisa calcular a pressão atmosférica no barômetro, pra ficar mais fácil de entender isso, vamos começar usando esse desenho:

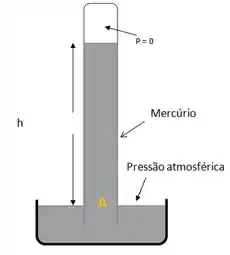
Para calcular a pressão atmosférica no local, temos que nos recordar que pontos localizados em um mesmo nível horizontal possuem a mesma pressão beleza?

Passo 2

Logo, tomando como referência o ponto A e um ponto localizado na superfície do mercúrio em contato com a atmosfera, temos:

p A = ρ g h =   p a t m o s f é r i c a

Como nesse caso h = 740,35   mm , temos:

p a t m o s f é r i c a = 1,3608 ×   10 4  kg/m³ × 9,7835   m/s × 740,35 × 10 - 3   m

p a t m o s f é r i c a ≅ 98,56   kPa

p a t m o s f é r i c a = 98,56 × 10 3   Pa

A gente precisa da unidade em torr , e para isso vamos usar isso aqui:

1   torr - 133,33   Pa

x - 98,56 × 10 3   Pa

x = 98,56 × 10 3 133,33 = 739,2   torr

Logo:

p a t m o s f é r i c a ≅ 739,2   torr

Show!

Resposta

p a t m o s f é r i c a ≅ 739,2   torr

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em muitos filmes de aventura na selva, o herói e a heroína escapam dos bandidos escondendo-se embaixo d’água por longos períodos de tempo. Para isto, eles respiram através de grandes canudos verticais
As leituras dos barômetros são dadas, às vezes em polegadas de mercúrio (inHg). Determine a pressão, em polegadas de mercúrio, igual a 101 kPa.
A pressão na superfície de um lago é P a t m = 101k P a . A que profundidade a pressão é 2 P a t m ? Se a pressão na superfície de uma longa coluna de mercúrio é P a t m , a que profundidade a pressão
Quando uma mulher, em sapatos de salto alto, dá um passo, ela momentaneamente aplica todo o seu peso sobre um salto. Se a massa dela é 56,0 kg e a área do salto é de 1,00 cm², qual é a pressão exercid
Quando na altitude de cruzeiro, uma típica cabine de avião terá uma pressão do ar equivalente à de uma altitude de cerca de 2400m. Durante o vôo, acontece de os ouvidos estabelecerem um equilíbrio, de