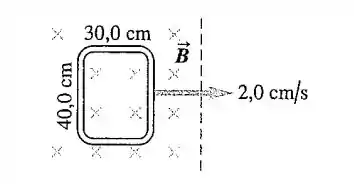
29.10. Um retângulo que mede 30,0 cm por 40,0 cm está localizado no interior de um campo magnético espacialmente uniforme de 1,25 T, com o campo perpendicular ao plano da bobina ( Figura 29.29). A bobina é retirada a uma taxa regular de 2,0 cm/s, se movendo perpendicularmente às linhas de campo. A região do campo termina abruptamente, conforme indicado. Determine a fem induzida nessa bobina quando ela está (a) inteiramente no interior do campo; (b) parcialmente no interior do campo; (c) inteiramente fora do campo.

Agora no caso do item (b), vai haver uma variação do fluxo magnético, então

Então agora temos um calculo para fazer, bom o fluxo magnético é calculado como

E a fem é calculada assim

Bom, de acordo com o enunciado, a área é variável. A bobina vai se afastando a uma taxa de ou seja . Como é um retângulo, e somente move-se em uma das componentes, a área pode ser calculada como

Ou no SI

Então podemos fazer

Bom, como depende do tempo, podemos usar a regra da cadeia

Então vamos derivar em relação a

Sabemos a taxa de variação de em relação ao tempo

E o enunciado também nos dá o valor do campo

Substituindo os valores, temos

Fazendo essa conta tempos

Agora no item (c) a situação é mesma que no item (a), o fluxo magnético é constante, e nesse caso, igual a zero. Então