Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas Desafiadores - Ex. 66
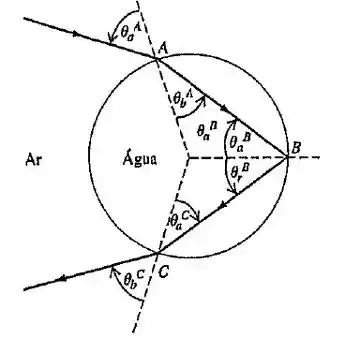
Um arco-íris é produzido pela reflexão da luz solar em gotas de água esféricas existentes no ar. A Figura 33.62 mostra um raio que se refrata para o interior de uma gota no ponto A, é refletido na superficie posterior da gota no ponto B e se refrata voltando para o ar no ponto C. Os ângulos de incidência e refração, e . são mostrados nos pontos A e C, os ângulos de incidência e de reflexão, , e ., são mostrados no ponto B. a) Mostre que e b) Mostre que o ângulo em radianos antes de o raio entrar na gota em A e depois de sair da gota em C (a deflexão angular total do raio) é . (Sugestão: determine a deflexão angular que ocorre em A, em B e em C e some para encon- trar .) c) Use a lei de Snell para escrever em termos de e de , o indice de refração da água na gota. d) O arco-íris se forma quando o angulo de deflexão é estacionário em relação a , . ou seja, quando . Quando essa condição for obedecida. todos os raios próximos de , sairão da gota retomando na mesma direção, produzindo una faixa brilhante no céu. Chame de , o ângulo para o qual isso ocorre. Mostre que (Sugestão: talvez voce ache conveniente usar a fórmula da derivada e) O indice de refração da água é igual a para a luz violeta e para a luz vermelha. Use os resultados dos itens (c) e (d) para calcular e para a luz vermelha e para a luz violeta. Seus resultados concordam com os angulos mostrados na Figura 33.20d? Quando você về um arco-íris primánio, qual cor está mais afastada do horizonte: a vermelha ou a violeta?
Passo 1
- Olhando para a figura do enunciado, temos que, devido os triângulos serem isósceles:
Mesmo para:
Usando igualdade de cima:
Aplicando a lei de snell no raio incidente à gota:
Aplicando a lei de snell no raio emergente à gota:
Como já vimos,
Então
Pela primeira lei de snell:
Então:
Prontinho!!
Passo 2
B)
Queremos a deflexão total dos raios incidente e emergente.
Vamos usar a dica que é calcular a deflexão que ocorre no ponto A, somar com a deflexão no ponto B e somar com a deflexão do ponto C.
Só lemrando que podemos entender deflexão como a mudança de direção que o raio tava fazendo. Tipo, se tinha uma raio vindo na horizontal e em um ponto ele passa a ir na vertical, então tivemos uma deflexão de . Show?
Vamos lá então!
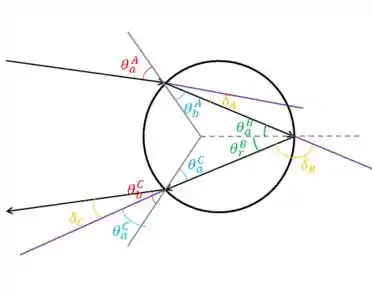
As retas em roxo são os prolongamentos.
Temos
Pelo item a, podemos escrever:
Show de bola!!
Passo 3
c)
Aplicando a lei de snell no raio incidente:
Então
Passo 4
d) Usando a condição:
Pela letra e, temos:
Podemos fazer uma substituição simples:
Então
Pela regra da cadeia
A derivada do :
Vamos voltar a substituição:
simplificando
Multiplicando todo mundo por
Elevando todo mundo ao quadrado:
Então
O ângulo para o qual isso ocorre é chamado de
Show!
Passo 5
e)
para o violeta.
Pelo item anterior:
Resolvendo:
E pelo item c:
Pela figura .
Vamos agora para o vermelho.
E
Pela figura .
Os ângulos concordam com os da figura. O do vermelho é maior que o do violeta, então o vermelho vai estar mais acima no horizonte.
Escrever só a resposta aqui quando o problema tiver resposta
Resposta
Ei, a resposta está no passo a passo :)