Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 3

Quantas imagens de uma fonte puntiforme situada entre dois espelhos que formam entre si um ângulo θ = 90 ° são produzidas? E se θ for = 120 ° ? Generalize para θ = 2 π / n , com n inteiro.

Passo 1

Vamos fazer um desenho da situação, colocar o observador e uns raios sendo refletidos.

A gente prolonga os raios refletidos, e onda há uma convergênia, é onde a imgem se forma.

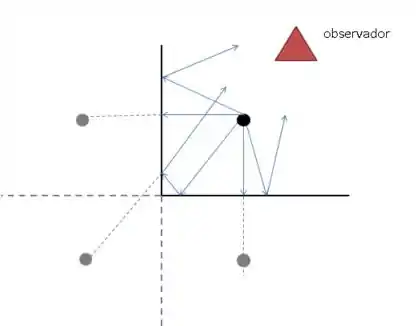
Com esse diagram de raios para nos auxiliar, vemos que o observador conseguirá ver 3 imagens do objeto.

Passo 2

Se os espelho estiverem com 120 ° entre eles, temos:

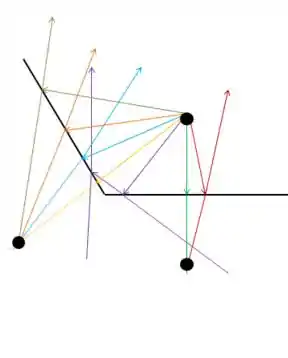
No mesmo esquema de antes, jogamos vários raios, e vemos onde há o ruzamento, nesses pontos ocorre a formação da imagem. Então, nesta situação temos que o observador consegue ver duas imagens.

Passo 3

Agora, vamos generalizar isso aí.

Para um ângulo de abertura θ , temos que n   imagens são formadas. O ângulo θ corresponde a uma parcela de um circunferência. Vamos analisar a rlação dessa parcela com o numero de imagens que podem ser vistas pelo observador.

θ = 360 ° n

Como, pelo menos uma imagem é formada, n ≠ 0 , e se temos dois espelhos com um θ ≠ 0 entre eles, então

n = 360 ° θ

Agora vamos ver como estamos indo. Para isso, vamos analisar os casos que já conhecemos.

Vimos que para θ = 90 ° → n = 3 . Então

n = 360 ° 90 ° = 4

Opa... vimos que o n deve ser três. Então a nossa generalização pode ser

n = 360 ° θ - 1

Vamos testar com θ = 120 ° .

n = 360 ° 120 ° - 1

n = 3 - 1

n = 2

Uhuul! Foi isso mesmo!

Então encontramos a regra geral.

Resposta

90 ° → 3 imagens

120 ° → 2 imagens

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No Exemplo 33.1, a interface água-vidro é horizontal. Se. em vez disso, a interface tivesse uma inclinação de 15 ° acima da horizontal, com o lado direito mais elevado do que o esquerdo. qual seria o
Prove que, quando um raio de luz incide sobre um espelho plano que gira em um ângulo θ em torno de um eixo perpendicular ao plano de incidência, o raio refletido gira em um ângulo igual a 2 θ .
Os três planos que convergem para um vértice interno de um cubo são revestidos por espelhos de modo que se forme um refletor de canto (veja o Exemplo 33.3 da Seção 33.2). Um raio de luz é refletido co
Um feixe de luz é orientado paralelamente ao eixo de um tubo cilíndrico oco. Quando o tubo contém apenas ar, a luz leva 8,72n s para atravessar toda a extensão do tubo, mas quando o tubo está cheio de
Um arco-íris secundário se forma quando a luz incidente sofre duas reflexões no interior de uma gota de água, como indicado na Figura 33.20e. (Veja o Problema desafiador 33.66.) a) Em relação ao ângul