Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 60
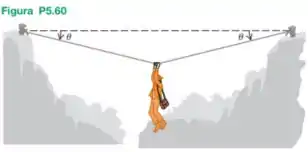
Um arqueólogo aventureiro passa de um rochedo para outro deslocando-se lentamente com as mãos por uma corda esticada entre os rochedos. Ele para e fica em repouso no meio da corda (Figura P5.60). A corda se romperá se a tensão for maior que e se a massa do nosso herói for de . (a) Se o ângulo for igual a , qual a tensão na corda? (b) Qual deve ser o menor valor de para a corda não se romper?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a tensão na corda quando o ângulo for igual a e determinar o menor valor de para a corda não se romper.
Essa é um problema bem tradicional de estática do ponto material e começamos sempre pelo diagrama de forças:
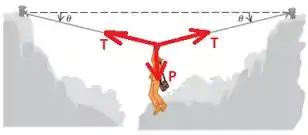
Onde temos o peso para baixo e as trações nas cordas. Como o homem está pendurado no meio da corda, as tensões se distribuem igualmente em ambos os lados da corda!
O segredo para resolver esse problema é decompor a tração:
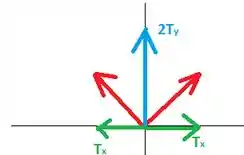
Fazendo a decomposição achamos as componentes da tensão:
As componentes se cancelam, enquanto as se somam, de modo que para o sistema ficar em equilíbrio devemos ter
Logo,
Essa é a equação que vamos usar para resolver o problema! Vamos lá!
Passo 2
No item (a) temos que , de modo que
Substituindo e , temos que
Fazendo as contas:
Passo 3
No item (b) nós queremos que a corda não se rompa, de modo que
onde . Com isso,
Portanto,
Usando uma calculadora, achamos que isso corresponde a
Logo, o menor valor de deve ser
Valeu, galera! Até a próxima! 😉