Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 23
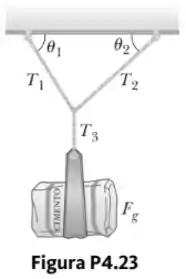
Um saco de cimento pesando está pendurado em equilíbrio por três cabos, como sugerido na Figura P4.23. Dois dos cabos formam ângulos e com a horizontal. Supondo que o sistema esteja em equilíbrio, encontre as tensões , e nos cabos.
Passo 1
E aii galera, tudo bem com vocês?
Vamos fazer mais uma questão?
Vem comigo!
Temos que .
Então, para
Passo 2
Como ,
Resposta
Exercícios de Livros Relacionados
Um macaco de 10k g sobe em uma árvore por uma corda de massa desprezível que passa por um galho sem atrito e está presa na outra extremidade a um caixote de 15k g , inicialmente em repouso no solo (Fi
A Fig. 5-58 mostra três blocos ligados por cordas que passam por polias sem atrito. O bloco B está sobre uma mesa sem atrito; as massas são m A = 6,00k g , m B = 8,00k g e m C = 10,0k g . Qual é a ten
Um bloco de massa M é puxado ao longo de uma superfície horizontal sem atrito por uma corda de massa m , como mostra a Fig. 5-63. Uma força horizontal F → age sobre uma das extremidades da corda. (a)
Na Fig. 5-59, o bloco A de 4,0k g e o bloco B de 6,0k g estão conectados por uma corda de massa desprezível. A força F → A = 12N i ^ atua sobre o bloco A ; a força F → B = 24N i ^ atua sobre o bloco B
A Fig. 5-57 mostra parte de um teleférico. A massa máxima permitida de cada cabina com passageiros é 2800k g . As cabinas, que estão penduradas em um cabo de sustentação, são puxadas por um segundo ca