Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 31

Um piano de 500   k g está sendo baixado por um guindaste enquanto duas pessoas o estabilizam puxando cordas amarradas nos lados do instrumento. A corda de Bob puxa o piano para a esquerda, com uma tensão de 500   N que forma 15 ° abaixo da horizontal. A corda de Ellen puxa o piano para a direita, formando 25 ° abaixo da horizontal.

  1. Que valor de tensão Ellen deve manter em sua corda a fim de manter o piano descendo com velocidade constante?
  2. Qual é o valor da tensão no cabo principal que sustenta o piano?

Passo 1

Vamos desenhar essa situação e as forças que estão atuando no piano:

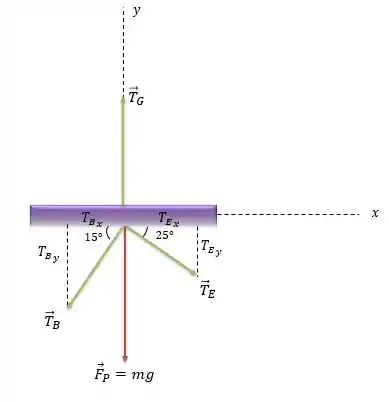
A força que atuam no piano são a força peso, a tensão na corda puxada por Bob, T → B , a tensão na corda puxada por Ellen,   T → E e a tensão feita pelo guindaste,   T → G .

Podemos decompor as tensões,   T → B e   T → E em componentes x e y como mostra o diagrama:

T B x = - T B   c o s   15 °

T B y = - T B sen ⁡ 15 °

T E x = T E   c o s   25 °

T E y = - T E sen ⁡ 25 °

Sempre lembrando daquele macete: COlada – COsseno, SEparada – SEno

Passo 2

  1. Que valor de tensão Ellen deve manter em sua corda a fim de manter o piano descendo com velocidade constante?

    2. Como a questão quer que o piano desça com velocidade constante, o somatório de todas as forças em cada direção tem que ser zero, para o piano está em equilíbrio:

    ∑ F x = 0

    ∑ F y = 0

    Vamos observar primeiro o eixo x :

    T B x + T E x = 0

    - T B   c o s   15 ° + T E   c o s   25 ° = 0

    T E   c o s   25 ° = T B   c o s   15 °

    Temos que:

    cos ⁡ 25 ° = 0,906

    c o s   15 ° = 0,966

    E o módulo da tensão na corda puxada por Bob foi dado na questão:

    T B = 500   N

    Então:

    0,906   T E = 500   x     0,966

    T E = 500   x     0,966 0,906

    T E = 533   N

    Passo 3

  2. Qual é o valor da tensão no cabo principal que sustenta o piano?

Agora vamos olhar para o eixo y :

T B y + T E y + T G - F P = 0

- T B sen ⁡ 15 ° -   T E sen ⁡ 25 ° + T G - m g = 0

T G = T B sen ⁡ 15 ° +   T E sen ⁡ 25 ° + m g

Temos que:

sen ⁡ 25 ° = 0,423

sen ⁡ 15 ° = 0,259  

m = 500   K g

g = 9,8   m / s 2  

T B = 500   N

T E = 533   N

Então:

T G = 500   x   0,259 + 533   x   0,423 + 500   x   9,8

T G = 5   255   N

Resposta

  1. T E = 533   N
  2. T G = 5   255   N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O aparato da Figura 4-60 é chamado de máquina de Atwood e é usado para medir a aceleração de queda livre g medindo-se a aceleração dos dois blocos ligados pelo fio que passa pela polia. Suponha uma po
O mastro de um veleiro é preso à proa e à popa por tirantes metálicos de aço inoxidável, um frontal e o outro traseiro, com as bases separadas de 10m (Figura 4-61). O mastro de 12m de comprimento pesa
Os blocos de massa m e 2 m estão sobre uma superfície horizontal sem atrito (Figura 4-66). Os blocos estão ligados por um fio horizontal. As forças F → 1 e F → 2 são aplicadas, conforme mostrado. (a)
O dispositivo da figura gira em torno do eixo vertical com velocidade angular ω . a) Qual deve ser o valor de ω para que o fio de comprimento l com a bolinha suspensa de massa m faça um ângulo θ com a
Um bloco de massa M é puxado ao longo de uma superfície horizontal lisa por uma corda de massa m, sobre a qual se exerce uma força horizontal F, conforme indica a figura. Determine a aceleração a do b