Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 40
Para arrastar um tronco de 75,0 kg no chão com velocidade constante, seu trator tem que puxá-lo com uma força horizontal de 250 N. (a) Desenhe o diagrama de corpo livre do tronco. (b) Use as leis de Newton para determinar a força de atrito sobre o tronco. (c) Qual é a força normal do chão sobre o tronco? (d) Qual força horizontal você deve exercer se deseja dar ao tronco uma aceleração de 2,00 m/s², supondo que a força de atrito não muda? Redesenhe o diagrama de corpo livre do tronco para esta situação.
Passo 1
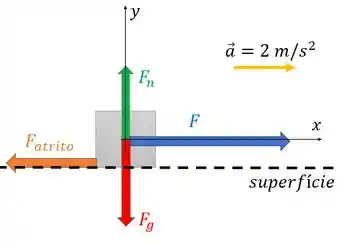
a) Oi pessoal, tudo bem? O tronco está sendo puxado com velocidade constante por uma força de . E nós queremos o diagrama de corpo livre.
Se ele está com velocidade constante significa que a aceleração sobre ele é nula, certo? Mas a força com que a gente puxa o tronco deve promover uma aceleração no tronco. Então porque a aceleração que ele tem é nula?
Cara, a única resposta que faz sentido é: há mais uma força sobre o tronco, oposta a . Que força? A força de atrito ! Ela vai resistir ao movimento de puxar o tronco. Assim, temos uma aceleração oposta a de , fazendo com a que a aceleração resultante no tronco seja nula.
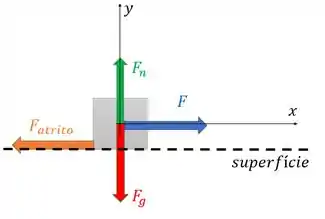
E o tronco está sobre uma superfície (já que há atrito), então há também a força normal que aparece por causa desse contato. Ela é perpendicular a superfície e aponta para cima. E por fim, há ação da gravidade, logo há força peso (já que o tronco tem uma massa).
Representando essas forças, nosso diagrama fica:
Passo 2
b) A força de atrito está na direção . Para descobrir o valor dela, a gente pode usar a segunda lei de Newton para essa direção:
Nessa direção, temos no sentido positivo de e no sentido contrario. Aí elas aparecem no somatório com sinais diferentes:
Vimos que o corpo está se movendo a uma velocidade constante, então . Substituindo ali em cima:
Como :
Passo 3
c) A força de normal está na direção . Para descobrir o valor dela, a gente pode usar a segunda lei de Newton para essa direção:
Nela, temos a força normal para o sentido positivo e a força peso para o sentido negativo de , por isso essa última aparece com sinal negativo no somatório de forças dessa direção:
A direção não há movimento, porque o tronco só se move na horizontal. Logo, não temos aceleração nessa direção também, ou seja . Substituindo:
Mas vamos lembrar que a força peso tem a expressão , substituindo isso na nossa equação:
Substitiundo nossos dados e lembrando que o tronco tem e que a aceleração da gravidade é :
Passo 4
d) Então, para que haja uma aceleração resultante não nula sobre o tronco, é preciso que a força seja maior que a força de atrito. Para representar isso num diagrama, a gente desenha o vetor de maior que o de :
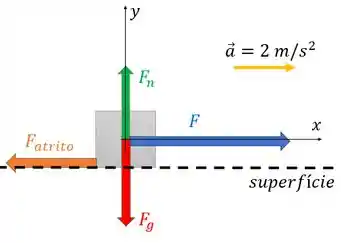
E para descobrir o novo valor de , vamos usar a segunda lei de Newton de novo para a direção :
Agora temos . Substituindo isso os outros dados:
-
Resposta
