Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 4.Problemas - Ex. 54
Uma caixa de 8,00 kg se encontra sobre um piso nivelado. Você dá um empurrão brusco na caixa e descobre que ela escorrega por 8,22 m em 2,8 s antes de parar novamente. (a) Você mede isso com um empurrão diferente e a caixa percorre 4,20 m em 2,0 s. Você acha que a caixa tem uma aceleração constante enquanto diminui a velocidade? Explique seu raciocínio. (b) Você acrescenta livros na caixa para aumentar sua
massa. Repetindo o experimento, você dá um empurrão na caixa e mede o tempo necessário para que ela pare e a distância que ela percorre. Os resultados, incluindo o experimento inicial, sem a inclusão de mais massa, aparecem nesta tabela:
Em cada caso, seu empurrão deu à caixa a mesma velocidade inicial? Qual é a razão entre a maior velocidade inicial e a menor velocidade inicial para esses quatro casos? (c) A força média horizontal f exercida sobre a caixa pelo piso é a mesma em cada caso? Represente graficamente o módulo da força f contra a massa total m da caixa mais seu conteúdo, e use seu gráfico para determinar uma equação para f em função de m.
Passo 1
A caixa para, então ela deve ter aceleração, então a segunda lei de Newton se aplica. Para
aceleração constante, as fórmulas cinemáticas padrão se aplicam.
Para aceleração constante, se aplicam. Para qualquer.
Passo 2
Letra a:
Se a caixa para com aceleração constante, sua velocidade final é zero, então . E se durante este tempo ele percorrer uma distância , a fórmula de distância acima pode ser colocada na forma .
Isso nos dá:
Para o primeiro empurrão na caixa, isso nos dá . Se a aceleração for constante, a distância que a caixa deve percorrer depois do segundo empurrão é , que é na verdade a distância que a caixa fez. Portanto, a aceleração foi constante.
Passo 3
Letra b:
Como , então .
Com os valores, chegamos em:
E assim, temos as massas:
em que todas as respostas foram arredondadas para 2 algarismos significativos. Podemos ver que a velocidade inicial era não a mesma em cada caso. A relação entre a velocidade máxima e a velocidade mínima é
Passo 4
Letra c:
Calculamos a magnitude da força usando e obtendo a usando , como mostramos antes. Em cada caso, a aceleração é . Então, por exemplo, quando , a força é .
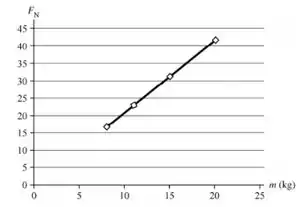
Cálculos semelhantes produzem um conjunto de valores para f e m. O gráfico resultante é mostrado na figura. A inclinação desta reta é e passa pela origem, então a equação
de interceptação da reta é .
