Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 4.Problemas - Ex. 37
O arremesso de beisebol mais rápido foi medido a 46 m/s. Uma bola de beisebol comum tem massa de 145 g. Se o arremessador exerceu sua força (considerada horizontal e constante) por uma distância de 1,0 m, (a) que força ele produziu sobre a bola durante seu arremesso recordista? (b) Desenhe diagramas do corpo livre da bola durante o arremesso e logo após ela ter deixado a mão do arremessador
Passo 1
Usando a cinemática de aceleração constante, podemos encontrar a aceleração da bola. Então nós podemos aplicar a segunda lei de Newton para encontrar a força que causa essa aceleração
Use as coordenadas onde +x está na direção em que a bola é lançada. Também vamos usar e
Passo 2
Letra a:
Resolvendo para temos:
O diagrama de corpo livre para a bola durante o arremesso é mostrado na figura a.
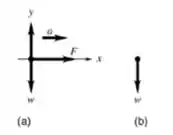
A força é aplicada à bola pela mão do arremessador.
Passo 3
Letra b:
O diagrama de corpo livre depois que a bola sai da mão é dado na figura b. A única força na bola é a força da gravidade para baixo.
A força é muito maior que o peso da bola porque dá a ela uma aceleração muito maior que g.
Resposta
- Ver desenhos