Um caminhão de entregas está transportando uma caixa de ferramentas, mas ele está sem a porta traseira. A caixa cairá do caminhão se ela começar a deslizar. Os coeficientes de atrito cinético e estático entre a caixa e o leito nivelado do caminhão são 0,355 e 0,650, respectivamente. Partindo do repouso, qual é o tempo mais curto que o caminhão poderia acelerar uniformemente até 30,0 m/s sem que a caixa deslize? Desenhe um diagrama do corpo livre da caixa de ferramentas.

Por um curto período de tempo, a aceleração é máxima, então a caixa de ferramentas está pronta para deslizar em relação à caçamba do caminhão. A caixa está em repouso em relação ao caminhão, mas está acelerando em relação ao chão porque o caminhão está acelerando. Portanto, a segunda lei de Newton será usada.

Se o caminhão acelerar para a direita, a força de atrito estático na caixa está para a direita, para tentar evitar que a caixa deslize em relação ao caminhão. O diagrama de corpo livre para a caixa é dado na figura:

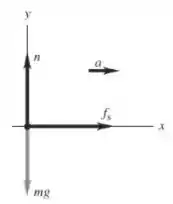
A aceleração máxima da caixa ocorre quando tem seu valor máximo, então .

Se a caixa não deslizar, sua aceleração é igual à aceleração do caminhão.

Vamos usar .