Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 8.Problemas - Ex. 77
Um automóvel sedan de entra em um cruzamento largo trafegando de norte a sul quando é atingido por um utilitário de trafegando de leste a oeste. Os dois carros se engavetam em decorrência do impacto e deslizam como se fossem um depois disso. Medições no local mostram que o coeficiente de atrito cinético entre os pneus desses carros e o pavimento é , e os carros deslizam até parar em um ponto a oeste e a sul do ponto de impacto. Qual era a velocidade de cada carro imediatamente antes da colisão?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a velocidade de cada carro imediatamente antes da colisão.
Para resolver esse tipo de problema o primeiro passo é fazer um esquema do que está acontecendo:
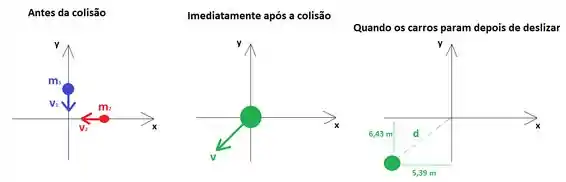
Antes da colisão o carro de massa se movimenta na direção com velocidade , enquanto o carro de massa se movia na direção com velocidade . Imediatamente após a colisão, o vetor velocidade do conjunto (que agora se move junto) é dado por .
Usando a conservação do momento linear, podemos escrever
Escrevendo , temos que
Um tempo depois, o sistema chega ao repouso depois de deslizar por uma distância , como mostrado na última figura. A direção do vetor é a direção que o conjunto se moveu, de modo que podemos escrever
Vamos guardar todas essas informações!
Passo 2
O módulo do vetor pode ser escrito como
Vale escrever também
Usando o teorema trabalho-energia entre a situação da figura e da figura , temos que
Como na situação final o sistema está em repouso, temos que , de modo que
Já o trabalho do atrito é:
Logo,
Portanto,
Substituindo os valores:
Com isso, podemos achar as componentes da velocidade e :
Passo 3
Agora que temos e , podemos achar e usando as relações do passo :
Assim,
Fazendo as contas, achamos
Valeu, galera! Até a próxima! 😉