Um avião a jato está voando a uma altura constante. No instante , os componentes da velocidade são , . No instante , os componentes são , . a) Faça um esboço do vetor velocidade para e para . Qual a diferença entre esses vetores? Para esse intervalo de tempo, calcule b) os componentes da aceleração média, c) o módulo, a direção e o sentido da aceleração média.

(a) Aqui, vamos apenas esboçar os vetores velocidade no dois instantes a partir de suas componentes. Sabendo que:

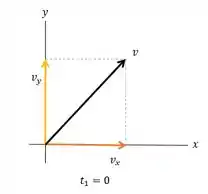
Para , temos .

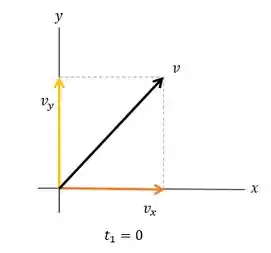
Para , temos

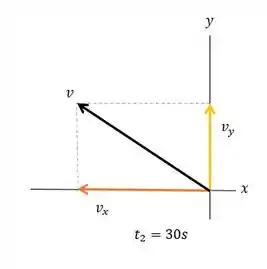
(b) A aceleração média pode ser calculada por:

O intervalo de tempo é:

Agora, vamos calcular :

No eixo , vamos ter:

No eixo :

Opa, agora podemos substituir os valores na equação de :

Agora que temos todos os valores necessários, vamos calcular o vetor aceleração média:

Substituindo o que encontramos:

Então, a componente da aceleração média é . E a componente é .

(c) Agora vamos utilizar a aceleração média que encontramos em cada coordenada para calcular o módulo da aceleração média. Faremos da seguinte forma:

Substituindo:

Para encontrar a direção, precisamos encontrar o ângulo da figura:

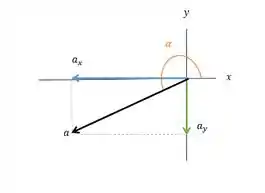
Podemos encontrar o ângulo entre e , que é o , e ele vai aparecer ali entre o e o .

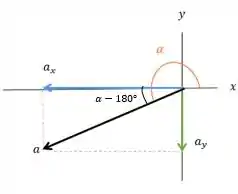
Como? Calculando a tangente dele! Vamos chama-lo de , ok? Então queremos que será:

Logo:

Maaaasss como , vamos achar o , que é o que nos interessa:

Então, temos uma aceleração direcionada em a partir do eixo positivo de .