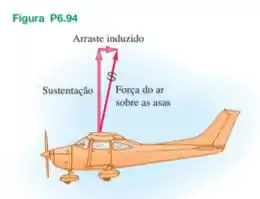
Quando um avião voa, está submetido a uma força de resistência do ar proporcional ao quadrado de sua velocidade . Porém, existe uma força de resistência adicional, pois o avião possui asas. O ar que circula sobre as asas é empurrado para baixo e ligeiramente para a frente, de modo que, pela terceira lei de Newton, ele exerce sobre as asas do avião uma força orientada para cima e inclinada ligeiramente para trás (Figura P6.94). O componente da força orientado para cima é a força de sustentação que mantém o avião suspenso no ar, e o componente da força orientado para trás denomina-se arraste induzido. Para velocidades de um voo típico, o arraste induzido é inversamente proporcional a , de modo que a força total de resistência do ar é dada por , onde e são constantes positivas que dependem da forma e do tamanho do avião e da densidade do ar. Para um Cessna 150, um pequeno avião monomotor, e . Em um voo com velocidade constante, o motor deve fornecer uma força orientada para a frente para igualar a força total de resistência do ar.  (a) Calcule a velocidade (em ) desse avião para o qual ele atinja um alcance máximo (isto é, atinja a distância máxima para uma dada quantidade de combustível). (b) Calcule a velocidade (em ) para que esse avião tenha a resistência máxima (isto é, para que ele permaneça no ar por mais tempo).

Passo 1

Passo 2

Passo 3

Resposta