Um balao de plastico que foi friccionado com lã adere a uma parede. a) Você pode concluir que a parede esta carregada? Se ela nao estiver, por que não? Se ela estiver, de onde veio a carga? b) Desenhe uma série de diagramas de carga que mostre como o balao adere a parede.
Passo 1
Fala galera, tudo bom com vocês?
Vem comigo pra fazer essa questãozinha aqui!
Letra a:
Não, não podemos concluir que a parede está carregada. Forças elétricas atrativas ocorrem entre (i) duas cargas opostas, ou (ii) uma carga e um objeto neutro que é polarizado pela carga. Esfregar o balão faz com que o balão carregue. Como o balão é de borracha, sua carga é negativa.
Conforme o balão é aproximado da parede, a parede torna-se polarizada. O lado positivo da parede está mais próximo do balão do que o lado negativo, então há uma força elétrica atrativa líquida entre a parede e o balão. Isso faz com que o balão grude na parede, com uma força normal equilibrando a força elétrica atrativa e uma força de fricção para cima equilibrando a força gravitacional pequena no balão.
Passo 2
Letra b:
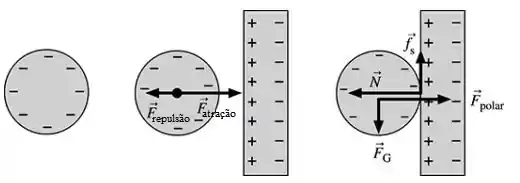
Resposta
Ver resolução