Uma barata grande pode desenvolver uma velocidade igual a em intervalos de tempo curtos. Suponha que, ao acender a lâmpada do quarto de um hotel à beira da estrada, você aviste uma barata que se move com velocidade de na mesma direção e sentido que você. Se você está a atrás da barata com velocidade de , qual deve ser sua aceleração mínima para que você alcance a barata antes que ela se esconda embaixo de um móvel situado a da posição inicial dela?
Passo 1
Falaaa, querido! Vamos fazer um esquema da nossa situação
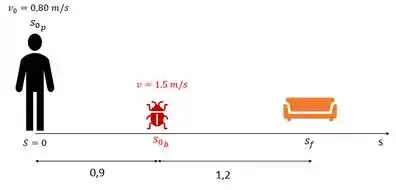
Você vê a barata e quer matar antes que ela vá para debaixo do móvel. Então a situação limite é que você e barata cheguem no móvel no mesmo instante, certo?
Então temos que a barata está em uma velocidade constante de e tem que percorrer .
Já você tem que pecorrer (resultado do somatório da sua distancia até barata e dela até o móvel) e dispara com uma velocidade inicial de .
Agora vamos as cálculos!
Passo 2
Começando pela barata! Ela tem um movimento uniforme, sem aceleração, temos podemos calcular o tempo que leva até o móvel por
Onde é a posição, é a posição inicial, a velocidade e o tempo.
Considerando a origem do nosso referencial na posição da pessoa, a posição inicial da barata é . Lembrando que ela está a :
Isso é, a barata chegará no móvel em .
Passo 3
A pessoa esta se movimentando em movimento retilíneo uniformemente variado (MRUV), já que ela tem uma aceleração. A equação horária é dada por:
Onde é a velocidade inicial e a aceleração.
E considerando que a chinelada será dada no exato momento em que a barata ia se esconder, e nesse momento ambas estavam na mesma posição, temos que a pessoa e a barata precisam chegar no móvel levando o mesmo tempo.
Então a gente pode substituir , e na equação horária da pessoa para ver que aceleração mínima ela precisa ter para chegar no móvel no mesmo instante que a barata
Isso é, a aceleração mínima da pessoa precisa ser de para conseguir acertar a barata antes dela se esconder no móvel.