Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 2.Problemas - Ex. 39
Uma bola acelera a partir do repouso a 0,500 m/s2 enquanto se move para baixo em um plano inclinado de 9,00 m de comprimento. Quando atinge o fundo, a bola rola para outro plano, ao qual chega em repouso após mover-se por 15,0 m naquele plano.
- Qual é a velocidade da bola na parte inferior do primeiro plano?
- Durante qual intervalo de tempo a bola rola para baixo no primeiro plano?
- Qual é a aceleração ao longo do segundo plano?
- Qual é a velocidade da bola na posição 8,0 m ao longo do segundo plano?
Passo 1
a. A situação é mais ou menos essa, amores:
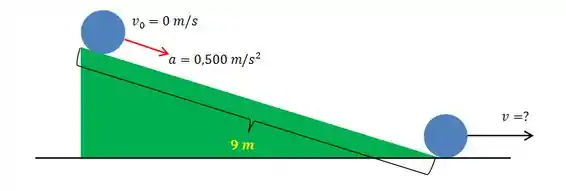
Beleza. Como a gente tem conhecidos a velocidade inicial (nula, pois parte do repouso), a aceleração e o deslocamento que a bola teve, e não temos o tempo que o percurso durou, o melhor aqui é usar Torricelli, olha só:
Vamos determinar , a velocidade ao fim de 9 metros de plano inclinado, aplicando os dados que já temos:
Passo 2
b. Agora, pra saber o tempo, a gente pode usar a formulinha do vovô ateu:
Determinamos a velocidade final, a inicial é o repouso e a aceleração a gente tem. Assim, o tempo vai ser a nossa incógnita! Vamos ter o seguinte, migos:
Passo 3
c. Então, se a gente já sabe a velocidade da bola quando ela chega no segundo plano, não inclinado, e se a gente considera que ela rola 15 metros até entrar em repouso de novo, o melhor pra gente é usar de novo Torricelli, já que não temos nada a respeito do tempo pra essa situação:
O agora é a nossa incógnita, e não é a mesma aceleração do caso anterior (não necessariamente!). A gente sabe a velocidade inicial (calculada no Passo 1), sabe que a velocidade final é nula e sabe o deslocamento de 15 metros.
Agora só aplicar, mores:
Esse sinal negativo indica que a bola está desacelerando, ou seja, perdendo velocidade, ok!
Passo 4
d. Bom, primeiro a gente precisa determinar em que instante a bola chegou na posição , tudo bem? Pra isso, como o movimento é (des)acelerado, a gente tem que usar a fórmula do sorvetão:
Que ainda pode ser reescrita assim:
O sinal negativo indica pra gente que a bola vai perdendo velocidade, ok?
Aqui, o deslocamento é de 8 metros, a velocidade inicial a gente viu no Passo 1 e a aceleração a gente acabou de calcular no Passo 3. Pra determinar , temos o seguinte:
Se você ainda não reparou, vamos cair em uma equaçãozinha de segundo grau, mas vai ser de boa. Vamos só ajustar pra ficar no formato mais familiar, assim:
Aplicando bhaskara, vamos determinar :
Bom, como um tempo não pode ser negativo, a gente só pode considerar o seguinte :
Passo 5
Ok, agora que conhecemos o tempo que a bola leva pra chegar na posição , dá pra gente determinar a velocidade dela nessa posição, usando vovô ateu:
vai ser nossa incógnita, a gente já conhece, sendo e a aceleração também conhecemos, sendo , além de que acabamos de calcular no último passo.
Vamos aplicar tudo e, assim, a gente vai ter:
Resposta
a.
b.
c.
d.