Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 68

Uma barra de 500 g e 60 cm de comprimento gira em um plano horizontal em torno de um eixo que passa por seu centro. Ar comprimido, injetado através do eixo, passa por um pequeno orifício abaixo da barra e sai sob a forma de pequenos jatos de ar através de furos nas extremidades da barra. Os jatos são perpendiculares ao eixo da barra. Partindo do repouso, ao final de 10 s a barra gira com uma freqüência angular de 150 rpm.

a. Que intensidade de força cada jato de ar que escapa exerce sobre a barra?

b. Se o eixo de rotação estivesse localizado em uma das extremidades da barra, com os jatos de ar mantidos inalterados, qual seria a velocidade angular da barra ao final de 10 s de movimento?

Passo 1

Bom pessoal, nós temos uma barra de 500 g e 60   c m de comprimento em um plano horizontal, conforme o enunciado. Essa barra é um corpo sólido girando através de seu centro.

Vamos visualizar melhor:

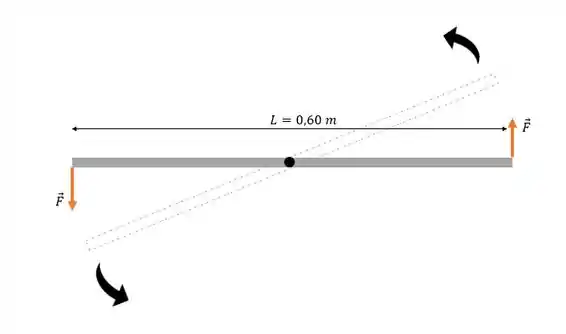
Passo 2

  1. As duas forças formam um casal. O torque total na barra sobre o centro é:

    2. τ t o t a l = L F = I α

    Isso implica que:

    F = I α L

    onde F é a força produzida por um dos jatos de ar. Podemos encontrar I e α da seguinte maneira:

     

    Primeiro I :

    I = 1 12 M L 2

    Substituindo pelos valores que temos:

    I = 1 12 0,50   k g 0,60   m 2 = 0,015   k g ⋅ m 2

    Agora α :

    vamos partir da seguinte equação:

    ω 1 = ω 0 + α ( t 1 - t 0 )

    Substituindo os valores que temos, ficamos com:

    150   r p m = 5,0 π   r a d / s = 0 r a d + α ( 10 s - 0 s )

    E então, isolando α :

    α = 0 , 50   π   r a d / s 2

    Passo 3

    Agora, podemos voltar a equação inicial, F = I α L , substituindo os valores e encontrar o que queremos, logo:

    F = ( 0,015   k g ⋅ m 2 ) ( 0,5   π   r a d / s 2 ) ( 0,60   m ) = 0,0393   N

    A força é F = 39   m N .

    Passo 4

  2. O torque de um casal é o mesmo em qualquer ponto. Ainda é τ t o t a l = L F . No entanto, o momento de inércia mudou.

τ t o t a l = L F = I α

Isolando α :

α = L F I

onde I = 1 3 M L 2 , então substituindo valores:

I = 1 3 0,500   k g 0,6 m 2 = 0,060   k g ⋅ m 2

Assim, voltando para a equação de α :

α = 0,0303   N × ( 0,60 m ) 0,060   k g ⋅ m 2 = 0,393   r a d / s 2

Passo 3

E finalmente,

ω 1 = ω 0 + α t 1 + t 0 = 0   r a d / s + ( 0,393   r a d / s 2 ) ( 10 s - 0 s )

⇒ ω 1 = 3,93   r a d / s = 3,93 60 2 π r p m = 37,5   r p m

A velocidade angular é de 38   r p m .

Passo 4

Observe que ω   ∝ α e α   ∝ 1   /   I . Assim, ω   ∝ 1   /   I .

I no centro da haste é 4 vezes menor que I em uma extremidade da haste. Consequentemente,   ω é 4 vezes maior.

Resposta

  1. A força é F = 39   m N .
  2. A velocidade angular é de 38   r p m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

95. Durante a maior parte de sua vida, uma estrela possui um tamanho de equilíbrio em que a força da gravidade sobre cada átomo, atraindo-o para dentro, é contrabalançada pela força de pressão, orient
90 . || Uma patinadora de 45k g está girando sobre as pontas de seus patins a 1,0r e v / s . Seus braços estão esticados ao máximo para fora do corpo. Nesta posição, a patinadora pode ser considerada
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que
67 . || Um bloco de 3,0k g é preso a um barbante que é enrolado ao redor de um cilindro oco de 2,0k g e 4,0c m de diâmetro, que pode girar livremente. (Use a F i g u r a12.34 , mas considere o cilindr