|| Um bloco de é preso a um barbante que é enrolado ao redor de um cilindro oco de e de diâmetro, que pode girar livremente. (Use a , mas considere o cilindro como oco.) O bloco é liberado acima do chão.
Use a segunda lei de Newton para determinar o valor da velocidade do bloco ao tocar o chão.
Use a conservação da energia para determinar o valor da velocidade do bloco ao tocar o chão.
Passo 1
Use a segunda lei de Newton para determinar o valor da velocidade do bloco ao tocar o chão.
Um esquema vai ser:
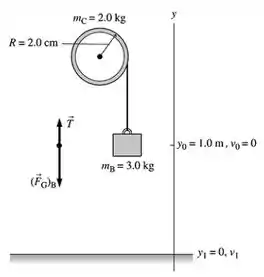
Passo 2
Considerando a força peso e a força de reação a 2 lei d Newton fica para o bloco na direção :
Mas
e
Então
Mas como um momento de inercia para um cilindro é:
Fica:
Passo 3
Agora que temos a aceleração, podemos usar Torricelli para movimento cilíndrico:
Passo 4
Use a conservação da energia para determinar o valor da velocidade do bloco ao tocar o chão.
Pela conservação de energia:
Fazendo Energia depois e antes:
O mesmo valor!!