Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 90

90 . || Uma patinadora de 45   k g está girando sobre as pontas de seus patins a 1,0   r e v / s . Seus braços estão esticados ao máximo para fora do corpo. Nesta posição, a patinadora pode ser considerada como tendo um tronco cilíndrico ( 40   k g , 20   c m de diâmetro médio e 160   c m de altura) mais dois braços do tipo barra (de 2,5   k g cada, com 66   c m de comprimento) fixados para fora do tronco. A patinadora, então, eleva os braços esticados para a posição vertical, posição em que ela parece ser um cilindro de 45   k g , com 20   c m de diâmetro e 200   c m de altura. Qual é a nova freqüência de rotação, em revoluções por segundo?

Passo 1

Um desenho para o problema é:

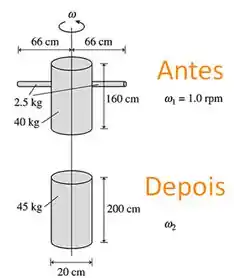
Passo 2

Podemos usar o momento angular inicial:

L i = I ω 0

Convertendo   ω 0  

ω 0 = 1 r e v / s = 6,28 r a d / s

E sabendo que o I se conserva:

I = I p a t i n a d o r a + I ( b r a ç o s )

I = m C r 2 2 + 2 1 12   m r l 2 + m r D 2

I = m C r 2 2 + 2 1 12   m r l 2 + m r l 2 + d 2 2

I = 40 ⋅ 0,1 2 2 + 2 1 12 ⋅ 2,5 ⋅ 0,66 2 + 2,5 ⋅ 0,33 + 0,1 2

I = 1306

Podemos fazer agora:

L i = I ω 0

L i = 1306 ⋅ 6,28

L i = 8,2 k g m 2 / s

Passo 3

O momento angular final será:

L f = 1 2 m r 2 ω f

L f = 1 2 45 ( 0.1 ) 2 ω f

L f = 0,225 ω f

Passo 4

Como os momentos angulares se conservam fazemos:

L f = L i

0,225 ω f = 8,2

ω f = 36,45 r a d / s

ω f = 5,8 r e v / s

Resposta

ω f = 5,8 r e v / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carrinho de brinquedo elétrico é colocado sobre um estreito trilho circular de 60 cm de diâmetro, cuja ranhura força-o a se mover em um círculo. O trilho, de 1,0 kg, é livre para girar em torno de
Conforme um motor a gasolina opera, um volante girando o virabrequim armazena energia depois de cada explosão de combustível, suprindo a energia necessária para comprimir a próxima carga de combustíve
Big Ben, o relógio da torre do Parlamento em Londres, tem o ponteiro menor (da hora) com 2,70m de comprimento e massa de 60,0k g , e o ponteiro maior (do minuto) com 4,50m de comprimento e massa de 10
Barras rígidas de massas desprezíveis localizadas ao longo do eixo y conectam três partículas (Fig.P10.18). O sistema gira no eixo x com velocidade angular de 2,00r a d / s . Encontre o momento de iné
Este problema descreve um método experimental para determinar o momento de inércia de um corpo de formato irregular tal como a carga de um satélite. A Figura P10.38 mostra um contrapeso de massa m sus