Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 10

Um bastão de vidro com 10   c m de comprimento está carregado uniformemente com   + 40   n C . Uma pequena conta de vidro, carregada com + 6,0   n C , encontra-se a 4,0   c m do centro do bastão. Qual é a força (módulo e orientação) exercida sobre a conta?

Passo 1

Faaaaaala, galera... Tranquileba??

Para encontrar o campo:

Fazendo um desenho do que o enunciado passa nós temos:

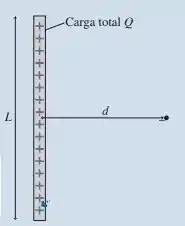
E pede-se então o campo. Bom, sabemos que as componentes em y se anulam existindo assim somente componentes em x. logo:

E x = E i cos i ⁡ θ = 1 4 π   ε 0   Δ Q r i 2 cos i ⁡ θ             ( 0.1 )

Sendo r i o modulo da distancia do ponto a um ponto quaisquer do bastão, assim:

r i 2   = R 2 + L 2

E R a distancia em x do bastão.

E sabemos também que:

cos i ⁡ θ = R R 2 + L 2

Assim:

E x = 1 4 π   ε 0   Δ Q R 2 + L 2 R R 2 + L 2 = 1 4 π   ε 0   Δ Q R R 2 + L 2 3 2           ( 0.2 )

Cada carga está relacionada por dy, de forma que:

Δ Q = λ d L

Sabemos que a densidade de cargas é:

λ = Q L

Assim:

Δ Q = Q L d L  

Logo em (0.2):

E x = 1 4 π   ε 0 1 L Q   d L R 2 + L 2 3 2

Pegando todo o espaço do bast - L 2 ≤ d L ≤ L 2

E x = 1 4 π   ε 0 Q L ∫ - L 2 L 2 d L R 2 + L 2 3 2    

Logo, resolvendo a integral simples temos que:

E x = 1 4 π   ε 0   Q R R 2 + L 2 2

Sendo a componente x a única não nula, logo:

E → = 1 4 π   ε 0   Q R R 2 + L 2 2   î

Passo 2

Feito isso, apliquemos os valores:

Sabendo antes que:

1 4 π   ε 0 = 9.0 × 10 9   N m 2 C 2

E → = 9.0 × 10 9   N m 2 C 2 ( 40 × 10 - 9   C 0.04   m 0.04   m 2 + 0.05   m 2 î = 1.406   × 10 5   N C

Passo 3

Sabendo que:

F → = q   E →

Portanto:

F → = 6,0 × 10 - 9   C 1.406   × 10 5   N C î = 8.4 × 10 - 4   î N

Resposta

F → = 8.4 × 10 - 4   î   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de comprimento l está uniformemente carregado com densidade linear de carga λ .Calcule o campo elétrico num ponto situado sobre o prolongamento do fio, a uma distância d da sua extremidade.Calc
Dois fios retilíneos de mesmo comprimento a , separados por uma distância b , estão uniformemente carregados com densidade lineares de carga λ e - λ (fig.) Calcule o campo elétrico no centro P do retâ
Um fio quadrado de lado 2 l está uniformemente carregado com densidade de carga linear λ . Calcule o campo elétrico num ponto situado sobre a perpendicular ao centro do quadrado, à distância D do seu
Um fio quadrado de lado 2 l está uniformemente carregado com densidade de carga linear λ . Calcule o campo elétrico num ponto situado sobre a perpendicular ao centro do quadrado, à distância D do seu
Uma camada infinita carregada compreendida entre os planos y = - a e y = a (fig.) tem densidade columétrica de carga ρ constante. Não há cargas fora dela. Calcule o campo elétrico E → dentro, acima e