Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 3
A barra horizontal da figura permanece na horizontal se (a) e , (b) , (c) , (d) , (e) .
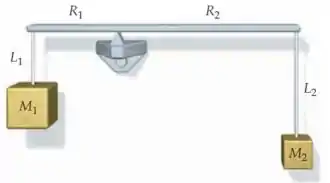
Passo 1
Se a barra não permanece na horizontal, isso quer dizer que ela terá sofrido uma rotação, certo? A única forma de impedir isso é garantir que o torque resultante seja nulo:
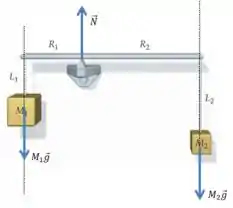
Passo 2
Então vamos calcular o torque resultante em relação ao ponto de apoio da barra.
Nesse caso, a força normal que age sobre a barra nesse ponto pode ser ignorado, porque o seu torque será nulo. Como as forças são perpendiculares à barra, a expressão para o torque será a seguinte:
Onde o torque de aparece com um sinal negativo porque favorece a rotação no sentido horário:
E então a condição é:
Resposta
Letra (b).
Exercícios de Livros Relacionados
Como a constante g é praticamente a mesma em todos os pontos da maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictíc
Uma caixa de massa desprezível está em repouso na extremidade esquerda de uma prancha de 2,0 m e 25,0 kg (Figura P11.43). A largura da caixa é 75,0 cm, e areia deve ser uniformemente distribuída dentr
Como a constante g é praticamente a mesma em todos os pontos da maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictíc
Como a constante g é praticamente a mesma em todos os pontos da maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictíc
Como a constante g é praticamente a mesma em todos os pontos da maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictíc