Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 7.Exercícios e Problemas - Ex. 10

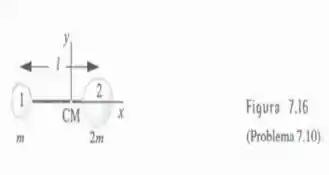
A barra que liga as duas esferas da Figura 7.16 tem massa desprezível. O corpo é abandonado no instante t = 0, com o centro de massa parado e girando no sentido anti-horário com velocidade angular w. A posição inicial do corpo é vista na figura. Estando o sistema sob a ação da gravidade, calcule:

A) A evolução temporal da posição do centro de massa, r C M ( t ) .

B) A evolução temporal da posição do centro da esfera 1, r 1 ( t ) .

Passo 1

Meus ferinhas, atenção.

A)

Atenção ao seguinte fato: a evolução temporal do centro de massa não dependerá da rotação das partículas, mas sim, apenas da gravidade e do tempo decorrido.

| r C M t | = | h t | = 1 2 g t 2

Como ele está caindo e o centro de massa é a origem dos eixos:

r C M t = - 1 2 g t 2 ∙ j

Passo 2

B)

A resolução da letra b é um pouco mais rebuscada, mas nada de demais!!!

Vamos.

Sabemos que:

r C M = 0

Já que o centro de massa é a origem dos eixos.

Sendo:

l 1 + l 2 = l

Logo:

0 = 2 m ∙ l 2 - m ∙ l 1 ( 2 m + m )

0 = 2 m ∙ l 2 - m ∙ l 1 3 m

0 = 2 l 2 - l 1

l 1 2 = l 2

Portanto:

l 1 + l 2 = l

l 1 + l 1 2 = l

l 1 = 2 3 ∙ l

Sendo l 1 o eixo de rotação da partícula 1.

Passo 3

B)

Sendo a fórmula:

r 1 t = R c o s w t ∙ i + R s e n w t ∙ j

Devemos considerar a evolução do centro de massa, logo:

r 1 t = R c o s w t ∙ i + R s e n w t ∙ j - g t 2 2 ∙ j

Notem um detalhe:

O conjunto está girando no sentido anti-horário e está caindo!!!

r 1 t = - 2 l 3 cos ⁡ w t ∙ i - 2 l 3 s e n w t + g t 2 2 ∙ j

Resposta

a )   r C M t = - 1 2 g t 2 ∙ j

b )   r 1 t = - 2 3 l . c o s w t ∙ i - 1 2 g t 2 + 2 3 l . s e n w t ∙ j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de 0,70k g está se movendo horizontalmente com uma velocidade de 5,0m / s quando se choca com uma parede vertical e ricocheteia com uma velocidade de 2,0m / s . Qual é o módulo da variação do
A Fig. 9-47 mostra uma vista superior da trajetória de uma bola de sinuca de 0,165k g que se choca com uma das tabelas. A velocidade escalar da bola antes do choque é 2,00m / s e o ângulo θ 1 é 30,0 °
No instante t= 0 , uma força F → 1 =( - 4 ,00i → +5 ,00j → )N age sobre uma partícula de massa 2,00 *10 - 3 k g , inicialmente em repouso, e uma força F → 2=( 2,00 i →-4,00 j → ) N age sobre uma partí
Uma colisão ocorre entre um corpo de 2,00k g que se move com uma velocidade v 1 =- 4,00 m s i →+ - 5,00 m s j → e um corpo de 4,00k g que se move com uma velocidade v 2=6,00 m s i →+ - 2,00 m s j → .O
Duas partículas,P e Q , são liberadas a partir do repouso a 1,0m de distância uma da outra. A partículaP tem uma massa de 0,10k g e a partícula Q tem uma massa de 0,30k g . P e Q se atraem com uma for