Exercícios de Velocidade e Momento Linear do Centro de Massa - Lista de Exercícios Resolvida

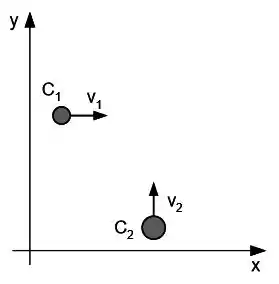
A figura mostra dois veículos que colidem de modo totalmente inelástico num cruzamento . A velocidade dos escombros conjuntos tem valor imediatamente após a colisão e direção que faz com o eixo . O veículo , que vinha no eixo da figura, tem massa , e o veículo tem massa . Considere o sistema isolado durante a colisão.

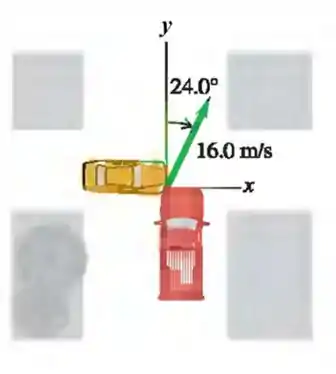
Forneça o vetor momento linear do centro de massa do sistema imediatamente depois da colisão, , e imediatamente antes da colisão, . Justifique.

Qual a velocidade escalar de cada veículo antes da colisão?

Forneça o vetor força que atuou sobre o veículo , , sabendo que a colisão teve duraçãoo de .

Um bloco deslocando-se com momento linear , colide com um bloco de momento linear , onde é constante. Suponha que não há força externa. Após a colisão o centro de massa do sistema segue, de acordo com o sistema de coordenadas ortogonais e os respectivos vetories unitários , e :

na direção e sentido negativo;

na direção e sentido negativo;

na direção e sentido positivo;

na direção e sentido positivo;

em uma direção formando um ângulo com os eixos e .

Um disco de massa , inicialmente em repouso sobre uma superfície horizontal sem atrito, sofre uma colisão não-frontal com um segundo disco de massa , movendo-se inicialmente ao longo do eixo com velocidade escalar constante . Após a colisão, o segundo disco passa a ter velocidade escalar e sai a um ângulo em relação ao eixo positivo, veja a figura. Use o sistema de coordenadas fornecido.

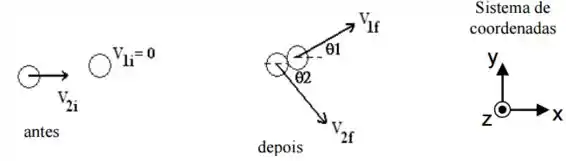
Ache o vetor velocidade do centro de massa dos discos antes da colisão.

Em termos dos vetores unitários e , determine o vetor velocidade do disco 1 após a colisão. Calcule o ângulo com que ele emerge.

Determine o vetor velocidade do centro de massa do sistema após a colisão, explicitamente usando seu resultado da letra . Compare com o resultado da letra e discuta.

Duas partículas e de massas e movem-se em movimento retilíneo uniforme com velocidades e respectivamente. Num dado instante ocorre uma colisão entre elas totalmente inelástica, pode-se afirmar, sobre a velocidade do centro de massa das partículas que:

Depois da colisão ;

Antes da colisão ;

Depois da colisão ;

Antes da colisão e depois da colisão ;

Depois da colisão ;

Um disco de borracha de se movimenta inicialmente com vetor velocidade sobre uma superfície horizontal sem atrito e sofre uma colisão com um disco de borracha de movendo-se inicialmente com vetor velocidade . Considere as seguintes situações:

Se o vetor velocidade e o vetor velocidade do centro de massa , calcule o vetor velocidade .

Um pescador está sentado no centro de sua canoa que repousa em um lago de águas tranquilas. A sua frente está um cesto com peixes a uma distância . Num dado instante ele muda a posição do cesto colocando-o detrás dele na posição . Considerando o centro de massa do sistema canoa-pescador-cesto e desprezando-se o atrito da água com a canoa, é correta a opção:

1. O centro de massa permanece na posição original;
2. O centro de massa move-se para frente de ;
3. O centro de massa move-se para trás de ;
4. Após mudar o cesto de posição a canoa passa a se movimentar com velocidade uniforme, pois a força resultante sobre o sistema é nula;
5. Nada se pode afirmar pois não são conhecidas as massas da canoa, do pescador e do cesto.

Duas partículas e de massas e movem-se em movimento retilíneo uniforme com velocidades e respectivamente. Num dado instante ocorre uma colisão entre elas totalmente inelástica, pode-se afirmar, sobre a velocidade do centro de massa das partículas que:

1. Depois da colisão ;
2. Antes da colisão ;
3. Depois da colisão ;
4. Antes da colisão e depois da colisão ;
5. Depois da colisão ;

Um rojão de massa explode após seu lançamento em apenas dois pedaços, um com o dobro da massa do outro. O rojão imediatamente antes da explosão tem velocidade e o pedaço de menor massa imediatamente após a explosão tem velocidade . A velocidade do pedaço de maior massa imediatamente após a explosão é

(a)

(b)

(c)

(d)

(e)

Duas partículas se deslocando em uma superfície horizontal sem atrito colidem elasticamente. Observando a colisão no referencial do Centro de Massa, analise as afirmações abaixo:

-O módulo da velocidade de cada uma das partículas é o mesmo antes e depois da colisão.

-Ambas as partículas se desviam de um mesmo ângulo de sua trajetória inicial.

-O momento linear total do sistema é nulo.

São corretas as afirmações:

1. Somente
2. Somente
3. Somente
4. Somente
5. Todas as afirmações.

Em um dado instante, o centro de massa de um sistema de duas partículas está localizado sobre o eixo no ponto e possui velocidade na direção positiva do eixo . Uma das partículas encontra-se na origem e a outra partícula possui massa e está em repouso sobre o eixo no ponto .

a) Qual a massa da partícula que está na origem?

b) Calcule o momento linear total do sistema.

c) Qual é a velocidade da partícula que está na origem?

Em um dos últimos jogos olímpicos de inverno, a final de Curling foi disputada entre Canadá e Rússia. O jogo consiste em posicionar pedras dentro de um alvo. Em uma de suas jogadas a equipe canadense realizou uma proeza típica de uma equipe vencedora. A figura abaixo representa a pista de gelo vista de cima. As duas pedras e da equipe russa estão em repouso e foram posicionadas durante o jogo. Uma terceira pedra a ser lançada pela equipe canadense está também ilustrada. A pedra lançada com velocidade , consegue acertar a pedra russa em uma colisão elástica bidimensional expelindo para fora do alvo com uma velocidade de módulo , sua trajetória faz um ângulo com a horizontal. Na sequencia a pedra faz uma segunda colisão elástica unidimensional com a pedra expelindo-a para fora do alvo. Considere todo atrito entre as pedras e o solo eliminado pelos outros membros das equipes com suas vassouras. Considere as massas de todas as pedras .

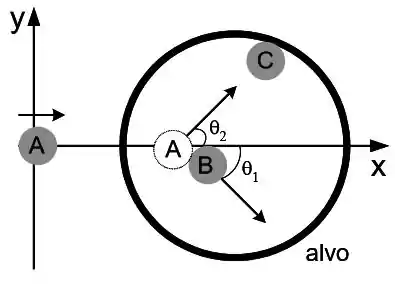
a) Determine a velocidade do centro de massa antes da primeira colisão.

b) Encontre o ângulo e a velocidade da pedra ao final da primeira colisão com a pedra .

c) Calcule a força média exercida pela pedra sobre a pedra durante a colisão que durou .

d) Considere agora a colisão entre as pedras e . Encontre e ao final da segunda colisão.

Seja um objeto de massa colocado no topo de um plano inclinado fixo de massa , base e altura . Considere o objeto como uma massa pontual e despreze o atrito entre o objeto e o plano inclinado.

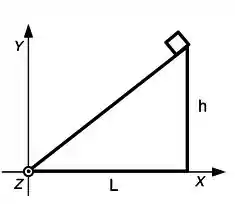
a) Determine a posição do centro de massa do conjunto (objeto + plano inclinado) na posição ao lado, antes do objeto ser solto. A posição do centro de massa do plano inclinado é dado por .

b) O objeto é largado do repouso de desce o plano inclinado. Determine a velocidade do centro de massa do conjunto imediatamente antes do objeto sair do plano inclinado.

Um cachorro de massa encontra-se parado na extremidade de um barco de massa () distribuída uniformemente em seu comprimento . O sistema encontra-se em repouso em um lago de águas calmas. Em um dado momento o cachorro se movimenta para a outra extremidade. Uma menina observa a situação às margens do lago, em repouso. Desprezando o atrito entre o barco e as águas do lago é incorreto afirmar que:

(a) O centro de massa do sistema barco-cachorro permanece em repouso durante o trajeto do cachorro.

(b) Para a menina o cachorro permanece em repouso enquanto o barco se move sobre as águas do lago.

(c) Para a menina, durante o trajeto do cachorro, o barco se movimenta no sentido oposto.

(d) Para a menina, o cachorro se move mais do que o barco.

(e) O momento linear do sistema cachorro-barco se conserva.

Um atleta com altura e massa se lança com uma velocidade sobre uma plataforma de comprimento e massa , inicialmente em repouso, que está sobre uma superfície de atrito desprezível. A plataforma entra em movimento horizontal e o atleta desliza sobre a superfície da plataforma até finalmente chegar em repouso em relação a ela. O coeficiente de atrito cinético entre o atleta e a plataforma é .

(a) Supondo que a componente do centro de massa do atleta esteja à da sua altura, calcule a posição do centro de massa do sistema (atleta + plataforma) no instante em que a componente do centro de massa do atleta estiver passando pela origem.

(b) Calcule a variação do momento linear do atleta e da plataforma. Porque o momento linear não se conservou no atleta e na plataforma?

(c) Calcule durante quanto tempo a força de atrito cinético atuou sobre o atleta supondo que a velocidade final do conjunto é .

(d) Que tipo de colisão ocorreu? Justifique sua resposta.

O bloco A, com massa de , está se movendo com velocidade de , enquanto o bloco B, com massa de , está se movendo em sentido oposto com velocidade de . O centro de massa do sistema dos dois blocos está se movendo com a velocidade de:

1. , no mesmo sentido de A;
2. , no mesmo sentido de A;
3. , no mesmo sentido de B;
4. , no mesmo sentido de B;
5. , no mesmo sentido de A;

Um disco de borracha de se movimenta inicialmente com vetor velocidade sobre uma superfície horizontal sem atrito e sofre uma colisão com um disco de borracha de movendo-se inicialmente com vetor velocidade . Considere as seguintes situações:

a) Se o vetor velocidade e o vetor velocidade do centro de massa , calcule o vetor velocidade .

b) Suponha que o vetor velocidade e que o vetor velocidade . Suponha também que após a colisão, o disco de tem velocidade escalar igual a e faz um ângulo em relação ao eixo positivo. Determine a velocidade do disco de após a colisão.

c) Suponha finalmente que o vetor velocidade e que o vetor velocidade e que a colisão é perfeitamente inelástica. Calcule a percentagem de energia perdida nesta colisão.

Em uma colisão bidimensional com força resultante externa nula, duas partículas de mesma massa, , colidem elasticamente como mostra a figura. Antes da colisão a velocidade da partícula 1 é e a partícula 2 está em repouso. O ângulo da velocidade com o eixo é .

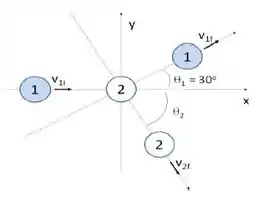
(a) Determine a velocidade da partícula 1 após a colisão.

(b) Obtenha o impulso sobre a partícula 1 durante a colisão.

(c) Encontre a velocidade inicial da partícula 2 em relação ao centro de massa do sistema.

Um sistema é constituído por duas partículas de massas e , ligadas por uma mola ideal, sobre uma mesa horizontal sem atrito. Em um determinado instante, o sistema está em repouso, com a mola distendida e uma força externa constante começa a ser exercida sobre a partícula de massa , na situação mostrada na figura a seguir.

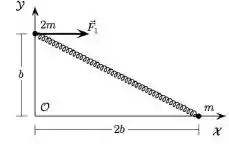
Que tipo de movimento o centro de massa do sistema formado pelas partículas e pela mola descreve?

(a) Movimento retilíneo uniformemente acelerado.

(b) Movimento retilíneo uniforme.

(c) Movimento circular uniforme.

(d) Movimento circular uniformemente acelerado.

(e) O centro de massa vai oscilar em torno da distância média entre as partículas.

(f) A trajetória será uma parábola.

Dois objetos de dimensões desprezíveis, de massas e , movem-se no plano , livres de forças externas, com velocidades e respectivamente, onde e representam os unitários dos eixos cartesianos. Supondo que os dois objetos se choquem numa colisão totalmente inelástica, determine

1. As velocidades do centro de massa do sistema, antes e depois da colisão;
2. Os momentos lineares e dos objetos, no referencial de centro de massa, antes da colisão.
3. Que fração da energia cinética é “perdida” com a colisão.

Uma granada está em repouso sobre uma mesa horizontal e sem atrito. Num dado instante ela explode em dois fragmentos de massas e velocidades diferentes, onde os fragmentos permanecem movimentando-se sobre a mesa. É possível afirmar que:

1. A energia cinética é conservada.
2. A posição do centro de massa das partículas varia com o tempo.
3. O momento linear total do sistema não é conservado.
4. A velocidade do centro de massa é nula após a explosão.
5. Nenhuma das opções acima está correta.

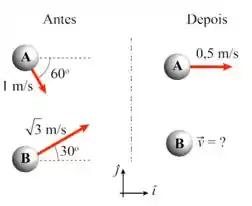
Duas partículas colidem numa superfície sem atrito. As velocidades de ambas antes da colisão são mostradas na figura ao lado. Após a colisão, a partícula A move-se com . Considere que a massa da partícula é o dobro da massa da partícula , ou seja, .

1. Qual é a velocidade do centro de massa do sistema antes da colisão?
2. Encontre o vetor velocidade da partícula B após a colisão.
3. A colisão é elástica? Justifique sua resposta

A figura mostra um sistema composto por duas partículas, de mesma massa , sobre as quais atuam forças, representadas pelas setas.

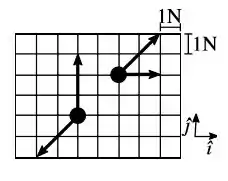
Nesta situação, a aceleração do centro de massa do sistema é igual a:

(a)

(b)

(c)

(d)

(e)

(f)

No referencial da Terra o está se aproximando com velocidade do , que está inicialmente em repouso. Os carros estão em um trilho de ar e o tem cinco vezes a inércia do . Eles colidem elasticamente. Calcule as velocidades antes e depois da colisão:

No referencial da Terra.

No referencial de momento zero.

Faça um gráfico do momento linear dos carros em função do tempo para o referencial de momento zero. Considere , e o tempo após a colisão. Coloque no gráfico os resultados para as velocidades obtidos no item precedente.

Uma partícula de massa se move com velocidade e aproxima-se de outra partícula de mesma massa que está parada em uma superfície sem atrito. As duas partículas colidem obliquamente. Logo após a colisão a primeira partícula passa a se mover com uma velocidade de módulo fazendo um ângulo de acima da direção de seu movimento antes da colisão. A segunda partícula logo após a colisão passa se mover com uma velocidade com módulo fazendo um ângulo de abaixo da direção inicial que tinha a primeira partícula antes da colisão.

(a) Determine a velocidade do centro de massa do conjunto logo após a colisão.

Dois corpos e se movem em um plano sem atrito. Suas posições variam no tempo e são dadas pelos vetores e , onde é dado em segundos e a posição em metros. O corpo tem massa e o corpo tem massa . Num dado instante de tempo, os dois corpos se chocam em uma colisão perfeitamente inelástica. Após a colisão, o vetor velocidade do conjunto faz um ângulo com a horizontal.

Calcule:

a) O vetor posição do centro de massa do sistema quando .

b) O vetor velocidade do centro de massa dos corpos na iminência da colisão.

c) O ângulo e o módulo da velocidade logo após a colisão.

d) A força que faz em durante a colisão que durou um décimo de segundo.

Dê as respostas em notação científica, no sistema internacional de unidades considerando rigorosamente o conceito de algarismos significativos.

Dois blocos de massa e separados por uma distância se movem no sentido do eixo positivo com e e vão sofrer uma colisão perfeitamente inelástica. Considere que no instante inicial o bloco de massa se encontre na origem do sistema de coordenadas na posição . Trate os blocos como massas pontuais.

a) Determine que é a equação que governa o movimento do centro de massa do sistema em função do tempo.

b) Determine o vetor velocidade final dos blocos após a colisão.

Numa superfície sem atrito, um bloco de massa está preso a uma mola de constante elástica e, inicialmente, encontra-se em repouso. Um bloco de massa , que se move com uma rapidez , colide com o primeiro bloco e fica grudado. A compressão máxima de mola é

(A)

(B)

(C)

(D)

(E)

Uma astronauta de está no espaço fazendo um reparo na estação espacial orbital. Ela lança fora uma ferramenta de a em relação à estação espacial. Qual será o módulo da velocidade e em que direção e sentido ela começará a se mover?

A posição de três partículas de massas e são dadas (no sistema SI) pelos seguintes vetores posição:

.

b. Há forças externas no sistema? Encontre a força externa ou argumente porque não há forças externas.

A posição de três partículas de massas e são dadas (no sistema SI) pelos seguintes vetores posição:

.

a. Determine a posição e a aceleração do centro de massa para um instante t qualquer;

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

b. Determine a velocidade de cada um dos corpos em relação ao centro de massa.

Dois blocos e de massas e , respectivamente, encontraram-se sobre uma superfície horizontal lisa. O bloco desloca-se com velocidade horizontal constante, enquanto o bloco encontra-se em repouso. Após a colisão os blocos separam-se e observa-se que o bloco de massa recua movendo-se com velocidade de módulo na mesma direção do seu deslocamento inicial, como mostra a figura.

1. Determine , o módulo da velocidade do bloco após a colisão.
2. Calcule o módulo da velocidade do centro de massa dos blocos antes e depois da colisão.
3. Determine a variação da energia cinética do sistema no processo da colisão.

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

c. Determine a energia cinética do movimento em relação ao centro de massa.

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

d. Determine a energia cinética do movimento do centro de massa.

Um carro de avança para oeste a e um caminhão, de , avança para leste com velocidade de . Determinar a velocidade do centro de massa do sistema.

Um sistema possui duas partículas que movimentam-se no plano . No instante, o centro de massa do sistema tem vetor posição , pois uma das partículas com massa está na origem e a outra, com massa , tem vetor posição . Sabendo que a velocidade instantânea do centro de massa do sistema é dada por , podemos afirmar que o módulo da força externa resultante que atua no sistema no instante , em Newtons, é:

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

a. Determine a energia cinética dos dois corpos nesse referencial e a velocidade do centro de massa.

Dois meninos com massas de 40kg e 60kg estão inicialmente em repouso sobre uma superfície horizontal sem atrito, segurando as extremidades de uma haste de massa desprezível e de 10m de comprimento. Os garotos puxam-se ao longo da haste. Quando eles se encontram, de quanto terá sido o deslocamento do menino de 40 kg?

a) precisa conhecer as forças que eles exercem

b) 4,0 m

c) 5,0 m

d) 6,0 m

e) 10 m

Uma partícula de massa move-se inicialmente com velocidade de módulo ao longo de uma trajetória retilínea que forma um ângulo de com o eixo , como mostra a figura. Ela colide com uma segunda partícula que tem duas vezes sua massa, isto é , que está movendo-se ao longo da direção e sentido positivo com velocidade de módulo três vezes maior que , ou seja: . Depois da colisão, a primeira partícula move-se ao longo da direção e sentido negativo, enquanto que a segunda partícula continua a mover-se ao longo do eixo e sentido positivo, com uma velocidade escalar reduzida. Considere que não atuam forças externas sobre as partículas. Se na solução de algum item abaixo for usada alguma lei de conservação, justifique-a.

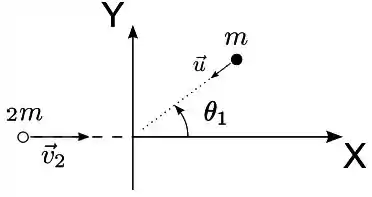
1. Determine o vetor momento linear total inicial para este sistema de duas partículas;
2. Calcule os módulos das velocidades de ambas as partículas depois da colisão em função dos dados do problema;
3. Determine o vetor velocidade do centro de massa do sistema antes e depois da colisão.

Dados: ; .

Assinale a alternativa verdadeira concernente ao centro de massa de um sistema de corpos.

(A) Toda a massa do sistema está concentrada em seu centro de massa.

(B) O centro de massa de um sistema pode estar localizado fora do sistema.

(C) Se aplicarmos forças externas ao sistema, o centro de massa não muda.

(D) A velocidade do centro de massa de objetos colidentes de um sistema pode mudar após a colisão.

(E) A velocidade do centro de massa de um sistema de corpos permanece constante se a resultante das forças externas aplicadas ao sistema for nula.

Em um dado instante , observa-se que duas partículas de massas e estão nas posições e movendo-se com velocidades e , respectivamente. Passados , elas são novamente observadas e vê-se que encontra-se parada. Sabendo-se que elas estão sujeitas somente a forças internas, o vetor posição do centro de massa (em metros) quando é:

(a)

(b)

(c)

(d)

(e)

Um menino encontra-se parado em uma das extremidades de um barco que está em um lago tranquilo. Inicialmente o conjunto (barco-menino) move-se com velocidade constante, em relação a um referencial inercial fixo colocado na margem do lago. Num dado instante o menino move-se para a outra extremidade do barco e ao chegar neste lugar ele para. Para o sistema barco-menino, desprezando-se o atrito entre o barco e a água, pode-se afirmar que

1. A sua velocidade antes do menino se movimentar é diferente de depois do menino parar.
2. A sua velocidade é a mesma de antes do início do movimento do menino e depois do menino parar.
3. A sua velocidade pode ser nula depois do menino parar.
4. Não se pode determinar a sua velocidade, pois não se conhece a velocidade do menino sobre o barco.
5. Não se pode determinar a sua velocidade, a menos que sejam conhecidas as massas do menino e do barco.

Em uma dada colisão bidimensional, uma bola de bilhar de massa , deslocando-se com velocidade atinge uma segunda bola idêntica, que está inicialmente em repouso, como ilustrado na figura abaixo. Após a colisão, a primeira bola passa a deslocar-se com velocidade de módulo , em uma direção que faz um ângulo de com eixo .

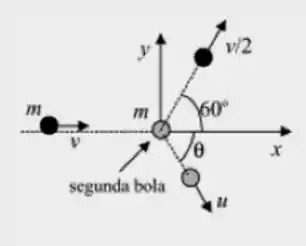
(a) Calcule o valor da velocidade da segunda bola imediatamente após a colisão (expresse seu resultado em termos de ).

(b) Tal colisão é elástica ou inelástica? Justifique quantitativamente sua resposta.

(c) Determine velocidade do centro de massa do sistema antes a depois da colisão. Justifique sua resposta.

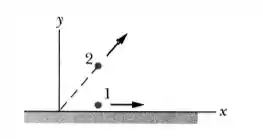
Na figura abaixo, duas partículas são lançadas da origem do sistema de coordenadas no instante . A partícula , de massa , é lançada horizontalmente para a direita, em um piso sem atrito, com uma velocidade escalar de . A partícula , de massa , é lançada com uma velocidade escalar de e um ângulo tal que se mantém verticalmente acima da partícula .

1. Qual é a altura máxima alcançada pelo CM do sistema de duas partículas?

Em termos dos vetores unitários, quais são

2. a velocidade e
3. a aceleração do CM ao atingir a altura máxima ?

Um automóvel de está em repouso em um semáforo. No instante em que a luz fica verde, o automóvel acelera constantemente a . No mesmo instante um caminhão de , movendo-se no mesmo sentido com velocidade constante de , ultrapassa o automóvel.

(a) Qual é a distância entre o CM do sistema carro-caminhão e o sinal de trânsito em ?

(b) Qual é a velocidade do CM nesse instante?