Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.9 - Ex. 23

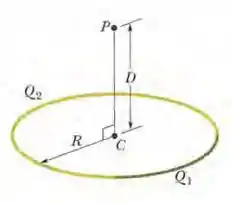
Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 = - 6 Q 1 distribuída uniformemente ao longo do resto da circunferência (figura abaixo). Com V = 0 no infinito, determine o potencial elétrico

(a) no centro C da circunferência;

(b) no ponto P, que está no eixo central da circunferência a uma distância D = 6,71 cm do centro.

Passo 1

Letra (a)

Mini-macete para a letra (a) e para a letra (b): Sempre que uma distribuição de cargas estiver a uma mesma distância de um ponto, o potencial nesse ponto pode ser calculado por essa fórmula:

V = K R ∑ i = 1 n q i

Passo 2

Pela dica, só precisamos fazer:

V = K R Q 1 + Q 2 = K R Q 1 - 6 Q 1 = - 5 K R Q 1

Passo 3

Substitua os valores:

V = - 5 8,99.10 9 N m 2 C 2 8,20.10 - 2   m 4,20.10 - 12   C = - 2,30   V

Passo 4

Letra (b)

Pelo mini-macete que a gente viu na letra (a), podemos repetir a ideia para o ponto P. O ponto P está na mesma distância de todos os pontos da circunferência. E essa distância, por Pitágoras, é igual a R 2 + D 2 .

Passo 5

Joga essa distância na fórmula:

V = K R 2 + D 2 Q 1 + Q 2 = K R 2 + D 2 Q 1 - 6 Q 1 = - 5 K R 2 + D 2 Q 1

Passo 6

Substitua os valores:

V = - 5 8,99.10 9 N m 2 C 2 8,20.10 - 2   m 2 + 6,71.10 - 2   m 2 4,20.10 - 12   C = - 1,78   V

Resposta

Letra (a): V = - 2,30   V

Letra (b): V = - 1,7 8   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Um disco de plástico de raio R = 64,0 cm é carregado na face superior com uma densidade superficial de cargas uniforme u = 7,73f C / m 2 e, em seguida, três quadrantes do disco são removidos. A Fig. a
A Fig. abaixo mostra uma barra fina com uma densidade de cargas uniforme de 2,00 μC/m. Determine o potencial elétrico no ponto P se d= D = L/4,00.
A barra fina de plástico que aparece na Fig. abaixo tem um comprimento L = 12,0 cm e uma densidade linear de cargas não uniforme λ = c x , onde c =28,9p C / m 2 . Com V =0 no infinito, determine o pot