Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.Problemas Adicionais - Ex. 74

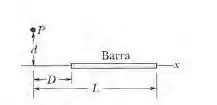
A Fig. abaixo mostra uma barra fina com uma densidade de cargas uniforme de 2,00 μC/m. Determine o potencial elétrico no ponto P se d= D = L/4,00.

Passo 1

Olá, meu nobre amigo. Yuri aqui estarei te ajudando a resolver essa atividade. Aqui deveremos encontrar o potencial elétrico num pontado dado, potencial esse gerado por uma barra.

Para essa questão, usaremos a fórmula do potencial de uma barra condutora fina de comprimento L   a uma distância d   da extremidade e que possui uma densidade linear de cargas λ .   Essa fórmula encontra-se no livro na equação 24-35. Porém, a gente tem que mudar o limite inferior de integral, já que no livro, ele considera que a extremidade da barra está “colada” na origem.

Passo 2

Então, alterando o limite de integração dessa equação:

V = ∫ L 0 L 1 4 π ϵ 0 λ d x x 2 + d 2 1 2  

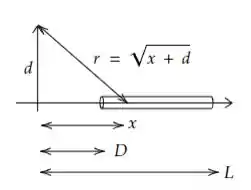
L 0 é a distância da extremidade da barra até a origem. Nesse exercício é D . Então substituindo na equação acima e desenvolvendo a integral:

V = ∫ D L 1 4 π ϵ 0 λ d x x 2 + d 2 1 2  

V =   λ 4 π ϵ 0 ∫ D L d x x 2 + d 2 1 2

V =   λ 4 π ϵ 0 ln ⁡ x + x 2 + d 2 1 2 D L

V =   λ 4 π ϵ 0 ln ⁡ L + L 2 + d 2 1 2 -   ln ⁡ D + D 2 + d 2 1 2

V =   λ 4 π ϵ 0 ln ⁡ L + L 2 + d 2 1 2 D + D 2 + d 2 1 2

Passo 3

Agora devemos substituir os valores que estão no enunciado e ser feliz:

V =   2,0 × 10 - 6 C m 4 π ϵ 0 ln ⁡ L + L 2 + L 4 2 1 2 L 4 + L 4 2 + L 4 2 1 2

V =   2,0 × 10 - 6 C m 4 π ϵ 0 ln ⁡ L + 17 L 2 16 1 2 L 4 + L 2 8 1 2 = 2,0 × 10 - 6 C m 4 π ϵ 0 ln ⁡ L + L 17 4 L 4 + L 2 2

V = 2,0 × 10 - 6 C m 4 π ϵ 0 ln ⁡ 4 L + L 17 L + L 2

V = ( 2,0 × 10 - 6   C / m ) 4 π ϵ 0 ln ⁡ 4 + 17 1 + 2 = 2,18 × 10 4   V

Resposta

V barra ⁡ = 2,18 × 10 4     V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio retilíneo infinito possui uma densidade linear de carga igual a 5 ⋅ 10 - 12 C / m . Um próton (massa 1,67 ⋅ 10 - 27 K g , carga + 1,6 ⋅ 10 - 19 C ) está a uma distância de 18 cm do fio e se des
Um anel fino uniformemente carregado possui raio de 15 cm e carga total igual a +24nC. Um elétron é colocado no eixo do anel a uma distância de 30 cm de seu centro, sendo obrigado a permanecer vincula
a)Mostre que V para uma casca esférica de raio R, com carga q uniformemente distribuída pela superfície, é o mesmo que V para um condutor maciço com raio R e carga q.b)Você atrita um balão inflado sob
Um cilindro muito longo, com raio de 2 cm, carrega uma densidade uniforme de 1,5 nC/m. a)Descreva o formato das superfícies equipotenciais para esse cilindro.b)Tomando como nível de referência para o
O campo elétrico na superfície de uma esfera carregada e maciça de cobre, com raio igual a 0,2 m, é 3800 N/C, orientado para o centro da esfera. Qual é o potencial no centro da esfera, caso se conside