Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.9 - Ex. 29

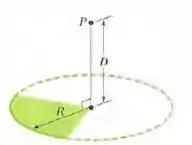
Um disco de plástico de raio R = 64,0 cm é carregado na face superior com uma densidade superficial de cargas uniforme u = 7,73   f C / m 2 e, em seguida, três quadrantes do disco são removidos. A Fig. abaixo mostra o quadrante remanescente. Com V = 0 no infinito, qual é o potencial produzido pelo quadrante remanescente no ponto P, que está no eixo central do disco original a uma distância D= 25,9 cm do centro do disco?

Passo 1

O enunciado nos passa uma informação bem importante: a carga no disco é uniforme. Isso significa que o potencial no ponto P produzido por esse quarto de disco é um quarto do potencial produzido pelo disco inteiro. Então, primeiramente, vamos calcular o potencial produzido por um disco inteiro.

Vamos pegar um anel de carga de raio r   e largura pequenininha d r . A área desse anelzinho é d A =   2 π r d r   e a carga é d q = σ d A ⇒ d q = 2 π r σ d r . Note que cada pedacinho desse anel está a uma distância r 2 + D 2   do ponto P. Então, o potencial que o anel produz no ponto P é:

d V = 1 4 π ϵ 0 2 π σ r d r r 2 + D 2 = σ r d r 2 ϵ 0 r 2 + D 2

Passo 2

Agora para saber o potencial do disco, basta integrar os infinitos anéis de r = 0   até r = R :

∫ 0 V d V = ∫ 0 R σ r d r 2 ϵ 0 r 2 + D 2 ⇒ V =   σ 2 ϵ 0 ∫ 0 R r d r r 2 + D 2 =   σ 2 ϵ 0 r 2 + D 2 ​ 0 R = σ 2 ϵ 0 R 2 + D 2 - D

Passo 3

Agora, basta dividir o potencial do disco por quatro para saber o potencial do disco V q e substituir os valores 😊:

V q = V 4 = σ 8 ϵ 0 R 2 + D 2 - D   = 7,73 × 10 - 15 C m 2 8 8,85 × 10 - 12 C 2 N . m 2 0,640   m 2 + 0,259   m 2 - 0,259   m = 4,71 × 10 - 5   V = 47,1   μ V

Resposta

V q = 4,71 × 10 - 5   V = 47,1   μ V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um anel com diâmetro de 8 cm está fixo em um ponto e carrega uma carga de + 5μ C , uniformemente espalhada sobre sua circunferência.a)Qual é o trabalho necessário para deslocar uma minúscula bola com
Uma casca cilíndrica isolante muito longa possui um raio de 6 cm e carrega densidade linear de carga de 8,5μ C / m uniformemente espalhada pela sua superfície externa. Qual seria a leitura de um voltí
Um cabo muito longo carrega uma densidade linear λ . Usando um voltímetro para medir a diferença de potencial, você observa que, quando uma sonda do aparelho é colocada a 2,5 cm do cabo e a outra sond
Duas placas metálicas paralelas grandes possuem densidade de cargas com mesmo módulo, mas sinais contrários (figura abaixo). Suponha que elas estejam próximas o suficiente para serem tratadas como pla
Um cilindro de carga isolante muito longo possui raio de 2,5 cm e carrega uma densidade linear uniforme de 15n C / m . Se você colocar uma sonda do voltímetro na superfície, a que distância da superfí