Generalize o resultado de Problema 13 ao caso da conduçõa do calor através de uma camada de material de condutividade térmica entre dois cilindros concêntricos de raios e e de comprimento , de modo que se possam desprezar os efeitos das extremidades. (a) Calcule a taxa de transmissão de calor por unidade de tempo através da camada. (b) Aplique o resutlado a uma garrafa térmica cilíndrica, com , e , com uma camada de ar entre as paredes interna e externa. A condutividade térmica do ar é de . A garafa contém café inicialmente a e a temperatura externa é de . Quanto tempo demora para que o café esfrie até a temperatura ambiente?
Passo 1
(a) Vamos resolver isso de um jeito bem parecido com o que fizemos no problema anterior. Começamos com um desenho da situação vista de cima:
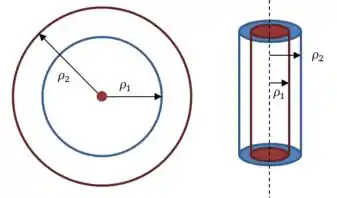
Já que o comprimento dos cilindros é muito maior do que os raios, estamos ignorando a condução de calor nas “tampas” e nas bases.
A ideia aqui é a seguinte: nós vamos calcular a taxa de transferência de calor por uma casca cilíndrica de raio e espessura .
A diferença de temperatura entre as faces dessa casca esférica é , então:
E a área de superfície é , então:
Essa taxa de transferência de calor deve ser a mesma em todos os pontos do cilindro (seja para uma casca ou para uma camada).
Essa é uma equação diferencial separável que nós podemos resolver para encontrar .
Passo 2
Começamos separando as variáveis:
E agora vamos integrar quando varia de até e varia de até :
Agora é só resolver as integrais:
E simplificando um pouco:
Passo 3
(b) Agora vamos calcular a taxa de transferência de calor no caso descrito no enunciado. Só precisamos substituir os valores numéricos, tomando muito cuidado com as unidades:
E então a energia perdida pela garrafa térmica durante um intervalo de tempo é:
Passo 4
E para calcular a variação de temperatura do café após perder todo esse calor, primeiro precisamos calcular a sua massa e calor específico.
O café que armazenamos em garrafas térmicas é quase totalmente composto de água, então podemos usar:
E se o café está em um cilindro de de raio e de altura, o volume total é:
E então a massa total é:
Passo 5
Agora sim, podemos calcular a variação de temperatura:
Queremos uma variação de temperatura de para :
Em horas, isso corresponde a:
Ou:
Resposta
(a) A taxa de transferência de calor é dada por .
(b) O café leva horas e minutos para esfriar até a temperatura ambiente.