Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 16.Problemas - Ex. 58
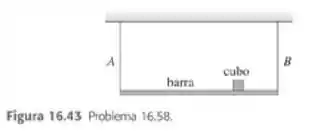
Uma barra uniforme de é sustentada horizontalmente por dois fios idênticos, e (Figura 16.43). Um pequeno cubo de chumbo de é colocado a do caminho entre e . Os fios medem cada um de comprimento e possuem uma massa de . Se ambos os fios são puxados simultaneamente em seu centro, qual é a frequência dos batimentos que eles produzirão ao vibrar em sua frequência fundamental?
Passo 1
Cada força sobre a barra produzirá torque nela, como a barra mantém um movimento harmônico, podemos dizer que não existe aceleração angular, então:
Vamos considerar que o eixo de rotação é o ponto onde o fio está pendurado (poderia ser o , não vai alterar o resultado).
Expressando cada torque na soma:
Como , ou seja, a distância entre a força aplicada e o ponto de rotação é zero, o primeiro termo some
Vamos considerar o sentido anti-horário como positivo, a equação fica:
Isolamos :
Agora a gente tem uma equação para encontrar a força que o fio faz sobre a barra. O peso e a distância do bloco são dados, o peso da barra também, e a distância do centro de massa até o ponto é , e . Substituindo tudo:
Cortando os comprimentos:
Passo 2
Agora vamos encontrar a força que o fio faz na barra. Como o movimento se mantém harmônico, as forças do sistema não aceleram e nem desaceleram a periodicidade, então podemos dizer que:
Caso alguma das forças produzisse uma aceleração em um sentido (para cima ou para baixo) as vibrações iriam parar o movimento ou produzir um torque total para um dos sentidos (horário ou anti-horário).
A soma das forças é:
As duas forças do final ficaram negativas porque o sentido delas é para baixo.
Isolando
Substituindo os valores:
Passo 3
Pronto, agora a gente tem as duas forças, podemos usar a equação de velocidade da onda em uma corda para cada uma:
E a equação das frequências para uma corda esticada:
Como queremos o modo fundamental:
Substituindo :
Escrevendo a densidade como:
Passo 4
Por fim, usamos a equação de batimentos:
E substituímos a frequência de cada corda:
Substituindo as forças, a massa das cordas e seus comprimentos: