Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 67

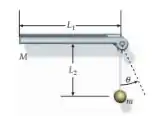
Uma barra uniforme, de comprimento L i e massa M igual a 0,75   k g , está presa a uma dobradiça de massa desprezível em uma das extremidades e é livre para girar no plano vertical (Figura 10-55). A barra é largada do repouso na posição mostrada. Uma partícula, de massa m = 0,50   k g , está suspensa da dobradiça por um fio fino de comprimento L 2 . A partícula gruda na barra quando as duas encostam. Qual deve ser a razão L 2 / L 1 para que θ m á x = 60 ° após a colisão?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Como o torque externo líquido que atua no sistema é zero, quantidade de movimento angular é conservada nessa colisão perfeitamente inelástica.

A haste, adquire energia cinética rotacional. O momento angular é conservado na colisão perfeitamente inelástica com a partícula, e a rotação cinética do sistema pós-colisão, é então transformada em energia potencial gravitacional à medida que o conjunto haste mais partícula balança para cima.

Usando conservação de energia mecânica temos:

K f - K i + U f - U i = 0

Como K i = 0 , temos:

K f + U f - U i = 0

1 2 I ω 2 + M g L 1 2 - M g L 1 = 0

1 2 ( 1 3 M L 1 2 ) ω 2 + M g L 1 2 - M g L 1 = 0

Logo:

ω = 3 g L 1  

Passo 2

Vamos agora chamar de ω ' , a velocidade angular do conjunto logo após o impacto. Usando conservação de quantidade de movimento angular, temos:

∆ L = L f - L i = 0

1 3 M L 1 2 + m L 2 2 ω ' - 1 3 M L 1 2 ω = 0

Logo:

ω ' = 1 3 M L 1 2 1 3 M L 1 2 + m L 2 2 ω

Aplicando conservação de energia mecânica novamente, temos:

K f - K i + U f - U i = 0

- 1 2 I ω ' 2 + M g 1 2 L 1 1 - cos ⁡ θ m á x + m g L 2 1 - cos ⁡ θ m á x = 0

Sabemos que:

I = 1 3 M L 1 2 + m L 2 2

Logo:

- 1 2 1 3 M L 1 2 + m L 2 2 1 3 M L 1 2 2   1 3 M L 1 2 + m L 2 2 2 ω 2 + 1 2 M g L 1 1 - cos ⁡ 60 ° + m g L 2 1 - cos ⁡ 60 ° = 0

- 1 2 1 3 M L 1 2 2   1 3 M L 1 2 + m L 2 2 3 g L 1 + 1 2 M g L 1 1 - 1 2 + m g L 2 1 - 1 2 = 0

- 3 g L 1 1 3 M L 1 2 2   1 3 M L 1 2 + m L 2 2 + 1 2 M g L 1 + m g L 2 = 0

Simplificando, obtemos:

L 1 3 = 2 m M L 1 2 L 2 + 3 m M   L 2 2 L 1 + 6 m M L 2 3

Passo 3

Podemos dividir os dois lados da equação por L 1 3 :

1 = 2 m M L 2 L 1 + 3 m M L 2 L 1 2 + 6 m M 2 L 2 L 1 3

Vamos chamar α = m / M e β = L 2 / L 1 :

1 = 2 α β + 3 α β 2 + 6 α 2 β 3

Sabendo que:

α = m M = 0,5   k g 0,75   k g = 0,667

Podemos então substituir os valores e chegar na sequinte equação do terceiro grau:

4 β + 6 β 2 + 8 β 3 - 3 = 0

Para resolver esta equação podemos aplicar o método de Newton-Raphson. Este método utiliza um processo interativo para aproximar-se de uma raiz de uma função:

β n + 1 = β n - f β n f ' β n

Temos que:

f β = 8 β 3 + 6 β 2 + 4 β - 3

E:

f ' β = 24 β 2 + 12 β + 4

Agora consideramos um β 0 = 1 , e fazemos as interações:

f β 0 = 1 = 8 1 3 + 6 1 2 + 4 ( 1 ) - 3

f β 0 = 1 = 15

Para a derivada, temos:

f ' β 0 = 1 = 24 1 2 + 12 ( 1 ) + 4

f ' β 0 = 1 = 40

Então, temos:

β 0 + 1 = β 0 - f β 0 f ' β 0

β 1 = 1 - 15 40

β 1 = 0,625

O erro da medida é calculado como:

∆ β 1 = 0,625 - 1 = 0,375

E ai você vai fazendo as interações até encontrar um erro aceitável. Geralmente fazemos as interações até que o erro seja da ordem de 10 - 6 .

Resolvendo a equação, temos:

β = 0,39

Portanto:

L 2 L 1 = 0,39

Resposta

L 2 L 1 = 0,39

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Uma bolinha de massa de modelar, de massa m , cai do teto sobre a borda de uma plataforma giratória de raio R e momento de inércia I o que gira livremente com uma rapidez angular ω 0 em torno do seu e
Suponha que, na figura, l = 0,60 m , L = 2,0 m , M = 0,80 k g e m = 0,40 k g . O fio se rompe quando a rapidez angular do sistema se aproxima de um valor crítico ω i , ao mesmo tempo que a tensão no f
Uma barra uniforme, de massa M e comprimento L , está sobre uma mesa horizontal sem atrito. Uma bolinha de massa de modelar, de massa m = M / 4 , move-se ao longo de uma linha perpendicular à barra. D