Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 78

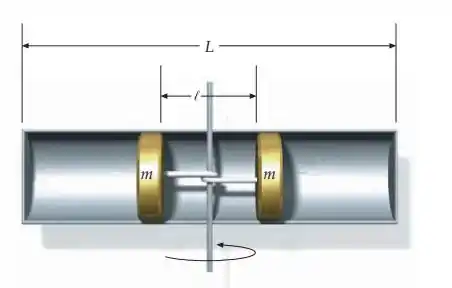
Suponha que, na figura, l = 0,60 m , L = 2,0 m , M = 0,80 k g e m = 0,40 k g . O fio se rompe quando a rapidez angular do sistema se aproxima de um valor crítico ω i , ao mesmo tempo que a tensão no fio se aproxima de 108 N . As massas, então, se afastam radialmente até sofrerem colisões perfeitamente inelásticas com as extremidades do cilindro. Determine a rapidez angular crítica e a rapidez angular do sistema quando a rapidez angular tem o valor crítico, e também, após as colisões inelásticas. Suponha ausência de atrito nas paredes internas do cilindro.

Passo 1

Concorda comigo que não tem nenhuma força externa atuando no sistema? Então também não tem torque! Então podemos conservar a quantidade de movimento angular!

Δ L = L f - L i = 0

I f ω f = I i ω i

ω f = I i I f ω i

Passo 2

Vamos calcular os momentos de inércia pra poder substituir na fórmula. O momento de inércia da situação vai ser a soma do momento de inércia do cilindro com o momento de inércia dos dois discos.

Na situação inicial:

I i = M L 2 10 + 2 m l 2 4

I i = 0.80 × 2 2 10 + 0.40 × 0.6 2 2

I i = 0.392   k g ⋅ m 2

Na situação final:

I f = M L 2 10 + 2 m L 2 4

I f = 0.80 × 2 2 10 + 0.40 × 2 2 2

I f = 1.12   k g ⋅ m 2

Passo 3

Agora a gente tem que encontrar a aceleração angular. Pra isso vamos olhar pro movimento circular, porque a tração no fio vai ser igual à aceleração angular.

T = m ω 2 r

T = m ω i 2 l 2

ω i = 2 T m l

Substituindo valores numéricos:

ω i = 2 × 108 0.40 × 0.60

ω i = 30   r a d / s

Passo 4

Com isso a gente substitui lá na primeira expressão que a gente encontrou:

ω f = I i I f ω i

ω f = 0.392 1.12 × 30 2

ω f = 1 0.5 r a d s

Passo 5

Falta só a gente calcular as energias. Tanto a final quanto a inicial são só energias rotacionais.

K i = I i ω i 2 2 = 0.392 × 30 2 2 = 176 J

K f = I f ω f 2 2 = 1.12 × 10.5 2 2 = 62 J

Resposta

ω i = 30 r a d s

ω f = 10.5 r a d s

K i = 176 J

K f = 62 J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra homogênea (de 0,60m de comprimento e 1,0k g de massa) da Fig. 11-54 gira no plano do papel em torno de um eixo que passa por uma das extremidades, com um momento de inércia de 0,12k g ∙ m 2 .
Na Fig. 11-56, uma criança de 30k g está em pé na borda de um carrossel estacionário de raio 2,0m . O momento de inércia do carrossel em relação ao eixo de rotação é 150k g ∙ m 2 . A criança agarra um
Um disco uniforme de massa 10 m e raio 3,0 r pode girar livremente como um carrossel em torno do centro fixo. Um disco homogêneo menor de massa m e raio r está sobre o disco maior, concêntrico com ele
Um trapezista pretende dar quatro cambalhotas em um intervalo de tempo ∆ t = 1,87s antes de chegar ao companheiro de número. No primeiro e no ultimo quarto de volta,mantem o corpo esticado como na Fig
Na Fig. 11-53, uma bala de 1,0g é disparada contra um bloco de 0,50k g preso à extremidade de uma barra não homogênea de 0,50k g com 0,60m de comprimento. O sistema bloco-barra-bala passa a girar no p