Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 87

Uma barra uniforme de comprimento L repousa sobre uma superfície horizontal sem atrito. A barra possui um pivô, de modo que ela pode girar sem atrito em torno de um eixo passando por uma das suas extremidades. A barra está inicialmente em repouso. Uma bala se deslocando com velocidade v ortogonal à barra e paralela à superfície atinge o centro da barra e permanece retida em seu interior. A massa da bala é um quarto da massa da barra.

a) Qual é a velocidade angular final da barra?

b) Determine a razão entre a energia cinética do sistema depois da colisão e a energia cinética da bala antes da colisão.

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que uma barra uniforme de comprimento L repousa sobre uma superfície horizontal sem atrito.

A barra possui um pivô, de modo que ela pode girar sem atrito em torno de um eixo passando por uma das suas extremidades.

A barra está inicialmente em repouso. Uma bala se deslocando com velocidade v ortogonal à barra e paralela à superfície atinge o centro da barra e permanece retida em seu interior.

Ah... a massa da bala é um quarto da massa da barra.

Queremos calcular a velocidade angular final da barra e a razão entre a energia cinética do sistema depois da colisão e a energia cinética da bala antes da colisão.

Bora lá entender isso melhor? 😉

Passo 2

  1. Vamos entender o que problema nos descreveu!

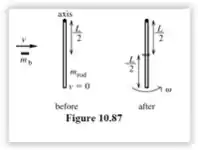
    2. Repara que a barra começa em repouso até que uma bala acerta-la, então ela gira com uma velocidade angular ω . Então temos duas situações: um início e um fim.

    Deste modo, usaremos a conservação do momento angular à colisão. Podemos perceber que o momento linear não é conservado. Por quê?? Por causa da força aplicada à haste no eixo.

    O problema nos diz que m b a l a = 1 4 m b a r r a . E temos que,

    L = m v r

    Onde L é o momento, m é a massa, v é a velocidade e r é o tamanho da barra (igual a L ).

    Para o inicio, temos

    L 1 = 1 4 m b a r r a v L 2

    L 1 = 1 8 m b a r r a v ( L )

    E para o final,

    L 2 = ( I b a l a + I b a r r a ) ω

    Onde I é o momento de inércia e ω é a velocidade angular.

    Como, o momento de inércia da barra é

    I b a r r a = 1 3 m b a r r a L 2

    E o da bala é

    I b a l a = 1 4 m b a r r a L 2 2 = 1 16 m b a r r a ( L ) 2

    Passo 3

    Igualando L 1 e L 2 :

    1 8 m b a r r a v L = 1 3 m b a r r a L 2 + 1 16 m b a r r a L 2 ω

    1 8 v = 19 48 L   ω

    ω = 6 v 19 L

    Passo 4

  2. A razão entre a energia cinética do sistema depois da colisão K 2 e a energia cinética da bala antes da colisão K 1 é

K 2 K 1

Onde:

K 1 = 1 8 m b a r r a v 2

K 2 = 1 2 I ω 2

Substituindo I e ω

K 2 = 1 2 1 3 m b a r r a L 2 + 1 16 m b a r r a L 2 6 v 19 L 2

K 2 = 1 2 19 48 m b a r r a L 2 6 v 19 L 2

K 2 = 3 152 m b a r r a v 2

Aplicando na razão:

K 2 K 1 = 3 152 m b a r r a v 2 1 8 m b a r r a v 2

K 2 K 1 = 24 152 = 3 19

Resposta

a) ω = 6 v 19 L

b) 3 19

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bicicleta tem rodas de 0,750 m de diâmetro. O ciclista acelera a partir do repouso, com aceleração constante, até 24,0k m / h , em 14,0 s . Qual é a aceleração angular das rodas?
Marte orbita em torno do Sol com um raio orbital médio de 228 G m ( 1 G m = 10 9 m ) e tem um período orbital de 687 dias. A Terra orbita em torno do Sol com um raio orbital médio de 149,6 G m . (a) A
Para ligar um cortador de grama, você deve puxar uma cordinha que está enrolada ao longo do perímetro de um volante. Depois de você puxar a corda por 0,95 s , o volante está girando a 4,5 revoluções p
Uma roda tem um aro fino de 3,0 k g e quatro raios, cada um com 1,2 k g de massa. Determine a energia cinética da roda quando rola a 6,0 m / s sobre uma superfície horizontal.
Determine a aceleração angular do cilindro do problema 96. Ele gira no sentido horário ou anti-horário? (b) Qual é a aceleração linear do cilindro (magnitude e orientação) em relação à mesa? (c) Qual