Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 59
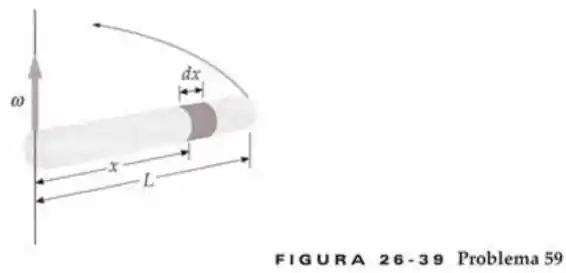
Um bastão fino uniforme e não condutor, om massa e comprimento , tem carga uniforme por unidade de comprimento e gira com rapidez angular em torno de um eixo que passa por uma extremidade e que é perpendicular ao bastão. (a) Considere um pequeno segmento do bastão de comprimento e carga a uma distância do pivô (Figura 26-39). Mostre que a corrente média criada pelo movimento pelo movimento deste segmento é e mostre que o momento magnético deste segmento é . (b) Use isso para mostrar que a magnitude do momento magnético do bastão é . (c) Mostre que o momento magnético e o momento angular estão relacionados por , onde é a carga total do bastão.
Passo 1
O elemento de carga executa um movimento circular de raio . O tempo para dar uma volta completa é
Assim, a corrente associada a esse movimento é
Desta forma,
Passo 2
O momento magnético associado a essa porção do fio é dado por
Assim,
Passo 3
Para achar o momento magnético total, temos que integrar de até :
Logo,
Passo 4
Para terminar temos que relacionar com o vetor momento angular . Cuidado para não confundir com , o enunciado não foi feliz na escolha das letras...
O momento angular é dado em função do momento de inércia por
Já o momento magnético é
Portanto,
O momento de inércia da barra com relação ao eixo é dado por
Se você não lembrar disso, dá uma olhadinha nos resumos de física 1. Com isso,
Mas a carga total é dada por
Assim,
Resposta
Demonstração.