Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 51
Um fio rígido tem o formato de um quadrado de lado . O quadrado tem massa e o fio conduz uma corrente . O quadrado está em uma superfície horizontal plana em uma região onde há um campo magnético de intensidade que é paralelo aos dois lados do quadrado. Qual é o valor mínimo de para que um dos lados do quadrado decole da superfície?
Passo 1
A figura a seguir ilustra o problema:
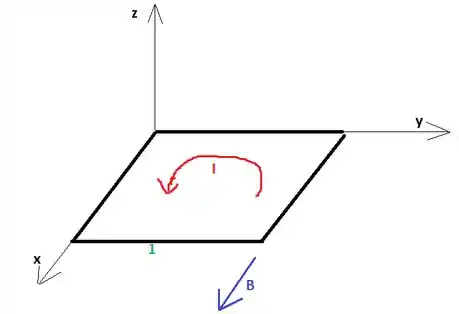
O campo magnético é dado por
Como a corrente gira no sentido anti-horário, usando a regra da mão direito vemos que o momento de dipolo magnético aponta na direção :
Com isso, o torque sobre a espira é
Passo 2
Além do torque devido ao campo elétrico, precisamos achar o torque do peso com relação ao eixo . O único torque importante é da barra marcada com 1, que será simplesmente o peso da barra () vezes o braço da força, que é :
A condição mínima para que o campo magnético faça a espira “saltar” é se o torque magnético igualar o torque do peso:
Daí,