Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 4ª Edição - Herch Moysés Nussenzveig- Ed: 4º - Capítulo 5.Problemas - Ex. 9
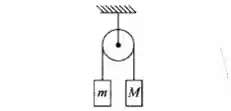
No sistema da figura ( máquina de Atwood) , mostre que a aceleração a da massa M e a tensão T da orda( desprezando as masss da corda e da polia) são dadas por
Passo 1
Vamos começar a analisar o problema pelo nosso diagrama de forças, beleza?
Nossas equações ficam assim
Isolando a tração na primeira equação e colocando na segunda temos
Passo 2
Se a gente quer descobrir a força de tração é só substituir de volta em uma das 2 equações, bora lá.
Aqui bora colocar o valor de encontrado antes
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Dois blocos de massa 3,50k g e 8,00k g são conectados por um fio sem massa que passa sobre uma polia sem atrito (Fig. P4.47). Os planos inclinados são sem atrito. Encontre o módulo da aceleração de ca
Na situação descrita no Problema 45 e mostrada na Figura P4.45, as massas da corda, balança de mola e polia são desprezíveis. Os pés de Nick não estão tocando o chão. Suponha que Nick esteja momentane
Na máquina de Atwood discutida no Exemplo 4.4 e mostrada na Figura Ativa 4.12a, m 1=2,00k g e m 2=7,00k g . Por comparação, as massas da polia e da corda são desprezíveis. A polia gira sem atrito e a
Uma criança inventiva chamada Nick quer pegar uma maçã em uma árvore sem escalá-la. Sentado em uma cadeira conectada a uma corda que passa sobre uma polia sem atrito (Fig. P4.45), Nick puxa a ponta so
Inicialmente, o sistema dos corpos mostrados na Figura P4.51 é mantido sem movimento. A polia e todas as superfícies não têm atrito. Seja a força F → zero e assuma que m 1 pode se mover apenas vertica