Um pintor está sobre uma plataforma suspensa de uma polia. Puxando a corda em 3, ele faz a plataforma subir com aceleração g/4. A massa do pintor é de 80 Kg e a da plataforma é de 40 Kg. Calcule as tensões nas cordas 1,2 e 3 e a força exercida pelo pintor sobre a plataforma.
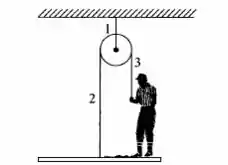
Passo 1
Vamos desenhar o diagrama de forças do nosso sistema
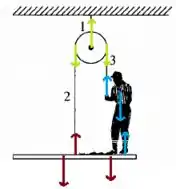
Todas as forças em azul são as que atuam sobre nosso pintor, elas são: seu peso, a tração da corda e a normal que a tábua exerce sobre ele. Sua equação fica assim
Já as forças marrons atuam na tábua e são: seu próprio peso, a tração da corda e a reação da normal do pintor, pela terceira lei de Newton. Então temos
Assim formamos um pequeno sistema
Já que e são um par de ação e reação tem o mesmo módulo, somando as 2 equações elas se cancelam e a gente chega nisso aqui,
Passo 2
Para achar a força que o pintor exerce sobre a tábua basta substituirmos de volta no nosso sistema, fica assim
Passo 3
Como já descobrimos a tração T em 3 e 2, basta somar as dua para obter a tração em 1, já que a polia está em equilíbrio de forças.